（安：原初我們是講有關「level」（境界）的問題。你用了「搞 gag」（弄笑話）來比喻。結果，這個「搞 gag」比喻發展出很多內容，可以獨立成篇。）

我就發覺我有這個能力：無論你給我什麼題目，大部分情況下，我也可以 generate（製作）出很多有趣的內容。我把這個能力叫做「話題魔法」。

而且，我還知道我懂「話題魔法」的原因。我把那些原因叫做「話題魔法理論」。

（安：那這個理論可以公開嗎？還是好像魔術師一樣，要遵守「魔法守則」，不可以公開魔術竅門？）

可以公開，不難解釋。我這個理論的靈感來自數學和物理。所以說，「讀得書多」是有用的。「讀得書多」令你多了很多神奇科幻的「思考工具」，去掌握日常生活的問題。

以下是「話題魔法理論」：

****************************************

以下是數學內容，沒有高等數學背景的朋友，可以把這部分略過：

每個「向量空間」都有很多 position vectors（位置向量）。但是，independent vectors（互相獨立的向量）其實很少。

例如，一個三次元空間有很多點（point），而每一點都可以用一支 position vector 來代表。所以，一個三次元空間有很多支 position vectors。但是，對於那個三次元空間來說，最多只能有三支 independent vectors。

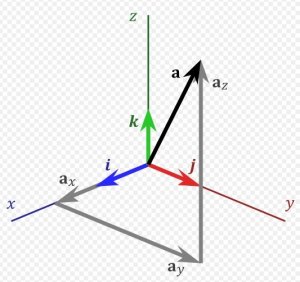
所以，要表達那個三次元空間的任何點的話，我沒有必要事先收集所有點的 position vectors。我需要的，只是三支 independent vectors，因為有三支 independent vectors (i, j, k) 的話，我就可以把任何 vector a 表達成 i, j, k 的線性組合（linear combination）：

a = a_x i + a_y j + a_z k = (a_x, a_y, a_z)

如果你只收集了兩支 independent vectors 的話，那就真是很抱歉，因為你不能表達三次元空間上所有點的 position vectors。例如，如果你只收集了 i, j 而沒有 k 的話，你只可以表達 x-y 平面上的點。那個平面以外的點，你通通不能表達。

對於三次元空間來說，｛i, j, k｝這三支 independent vectors 組成了一個 complete set（完備集合）。「完備」的意思是，只要有集合內的 vectors（i, j, k），就可以表達空間上任何一點的 position vectors。

— Me@2010.05.08

2010.05.09 Sunday (c) All rights reserved by ACHK