Functional Differential Geometry
.
The metric for a unit sphere, expressed in colatitude and longitude
, is
Compute the Lagrange equations for motion of a free particle on the sphere …
~~~
(define ((L2 mass metric) place velocity) (* 1/2 mass ((metric velocity velocity) place))) (define ((Lc mass metric coordsys) state) (let ((x (coordinates state)) (v (velocities state)) (e (coordinate-system->vector-basis coordsys))) ((L2 mass metric) ((point coordsys) x) (* e v)))) (define the-metric (literal-metric 'g R2-rect)) (define L (Lc 'm the-metric R2-rect)) (L (up 't (up 'x 'y) (up 'vx 'vy))) (show-expression (L (up 't (up 'x 'y) (up 'v_x 'v_y))))

.
(show-expression (L (up 't (up 'theta 'phi) (up 'thetadot 'phidot))))
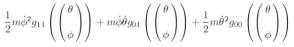
.
When and
,
.
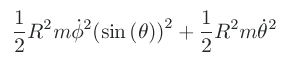
.
— Me@2022-10-27 10:30:50 AM
.
.
2022.10.28 Friday (c) All rights reserved by ACHK

You must be logged in to post a comment.