Ex 1.21 The dumbbell, 2.2.1

Structure and Interpretation of Classical Mechanics

b. Write the formal Lagrangian

$\displaystyle{L(t;x_0, y_0, x_1, y_1, F; \dot x_0, \dot y_0, \dot x_1, \dot y_1, \dot F)}$

such that Lagrange’s equations will yield the Newton’s equations you derived in part a.

~~~

[guess]


(define (U-constraint q0 q1 F l)
  (* (/ F (* 2 l))
     (- (square (- q1 q0))
        (square l))))

(define ((extract-particle pieces) local i)
  (let* ((indices (apply up (iota pieces (* i pieces))))
         (extract (lambda (tuple)
                    (vector-map (lambda (i)
                                  (ref tuple i))
                                indices))))
    (up (time local)
        (extract (coordinate local))
        (extract (velocity local)))))

(define q-rect
  (up (literal-function 'x_0)
      (literal-function 'y_0)
      (literal-function 'x_1)
      (literal-function 'y_1)
      (literal-function 'F)))

(show-expression q-rect)


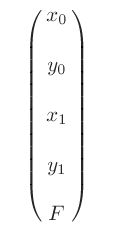
(show-expression (q-rect 't))


(show-expression (Gamma q-rect))


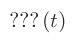
(show-expression ((Gamma q-rect) 'w))


(show-expression ((Gamma q-rect) 't))


(show-expression (time ((Gamma q-rect) 't)))


(show-expression (coordinate ((Gamma q-rect) 't)))

[guess]

— based on /sicmutils/sicm-exercises

— Me@2021-04-27 05:03:59 PM

Physics Town

continues

Ex 1.21 The dumbbell, 2.2.1

Related