Structure and Interpretation of Classical Mechanics

.

A particle of mass slides off a horizontal cylinder of radius in a uniform gravitational field with acceleration . If the particle starts close to the top of the cylinder with zero initial speed, with what angular velocity does it leave the cylinder?

~~~

(define ((KE m g R) local)
  (let ((t (time local))
        (thetadot (velocity local)))    
    (* 1/2 m (square R) (square thetadot))))

(define ((PE m g R) local)
  (let ((t (time local))
        (theta (coordinate local))
        (thetadot (velocity local)))    
    (- (* m g R (- 1 (cos theta))))))

(define L (- KE PE))

(show-expression
 ((L 'm 'g 'R)
  (->local 't
           'theta
           'thetadot)))

(show-expression
 (((Lagrange-equations
    (L 'm 'g 'R))
   (literal-function 'theta))
  't))

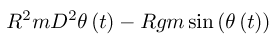
This derivation is wrong, because the constraint force is missing.

.

(define ((F->C F) local)
  (->local (time local)
           (F local)
           (+ (((partial 0) F) local)
              (* (((partial 1) F) local)
                 (velocity local)))))

(define (q->r local)
  (let ((q (coordinate local)))
    (let ((r (ref q 0))
          (theta (ref q 1))
          (lambd (ref q 2)))
      (let ((x (* r (sin theta)))
            (y (* r (cos theta))))
        (up x y lambd)))))

(show-expression
 (q->r
  (->local 't
           (up 'r 'theta 'lambda)
           (up 'rdot 'thetadot 'lambdadot))))

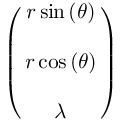
(define (KE m vx vy)
  (* 1/2 m (+ (square vx) (square vy))))

(define ((T-rect m) local)
  (let ((q (coordinate local))
        (v (velocity local)))
    (let ((xdot (ref v 0))
          (ydot (ref v 1)))
      (KE m xdot ydot))))

(show-expression
 ((T-rect 'm)
  (up 't
      (up 'x 'y 'lambda)
      (up 'xdot 'ydot 'lambdadot))))

(show-expression
 ((T-rect 'm)
  ((F->C q->r)
   (->local 't
            (up 'r 'theta 'lambda)
            (up 'rdot 'thetadot 'lambdadot)))))

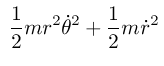
(define ((U-rect g m) local)
  (let* ((q (coordinate local))
         (y (ref q 1)))
    (* g (+ (* m y)))))

(define (L-rect g m)
  (- (T-rect m) (U-rect g m)))

(define (L g m)
  (compose
   (L-rect g m) (F->C q->r)))

(show-expression
 ((L 'g 'm)
  (->local 't
           (up 'r 'theta 'lambda)
           (up 'rdot 'thetadot 'lambdadot))))

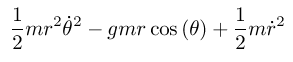
(show-expression
 (((Lagrange-equations
    (L 'g 'm))
   (up
    (literal-function 'r)
    (literal-function 'theta)
    (literal-function 'lambda)))
  't))

(define ((U-constraint R) local)
  (let* ((q (coordinate local))
         (x (ref q 0))
         (y (ref q 1))
         (lambd (ref q 2))
         (r_sq (+ (square x) (square y))))
    (* lambd (- r_sq (square R)))))

(define ((U2-constraint R) local)
  (let* ((q (coordinate local))
         (x (ref q 0))
         (y (ref q 1))
         (lambd (ref q 2))
         (r_sq (+ (square x) (square y))))
    (* lambd (- (sqrt r_sq) R))))

(define (L-rect-constraint g m R)
  (- (T-rect m) (+ (U-rect g m) (U-constraint R))))

(define (L2-rect-constraint g m R)
  (- (T-rect m) (+ (U-rect g m) (U2-constraint R))))

(show-expression
 ((L-rect-constraint 'g 'm 'R)
  ((F->C q->r)
   (->local 't
            (up 'r 'theta 'lambda)
            (up 'rdot 'thetadot 'lambdadot)))))

(show-expression
 ((L2-rect-constraint 'g 'm 'R)
  ((F->C q->r)
   (->local 't
            (up 'r 'theta 'lambda)
            (up 'rdot 'thetadot 'lambdadot)))))

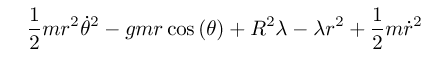
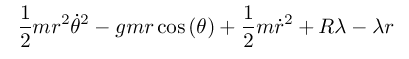
(show-expression
 (((Lagrange-equations
    (compose (L-rect-constraint 'g 'm 'R) (F->C q->r)))
   (up
    (literal-function 'r)
    (literal-function 'theta)
    (literal-function 'lambda)))
  't))

(show-expression
 (((Lagrange-equations
    (compose (L2-rect-constraint 'g 'm 'R) (F->C q->r)))
   (up
    (literal-function 'r)
    (literal-function 'theta)
    (literal-function 'lambda)))
  't))

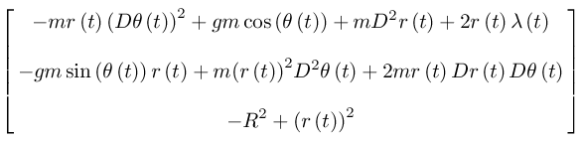
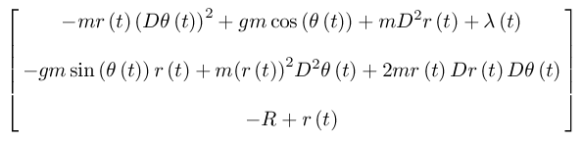
(show-expression
 (((Lagrange-equations
    (compose (L-rect-constraint 'g 'm 'R) (F->C q->r)))
   (up
    (lambda (t) 'R)
    (literal-function 'theta)
    (literal-function 'lambda)))
  't))

— Me@2023-07-12 10:00:19 PM

.

.

2023.07.13 Thursday (c) All rights reserved by ACHK