Daily Archives: October 9, 2022

Ex 1.1: Motion on a Sphere

Posted on by

Functional Differential Geometry

.

The metric for a unit sphere, expressed in colatitude \displaystyle{\theta} and longitude \displaystyle{\phi}, is

\displaystyle{g(u,v) = d\theta(u) d \theta(v) + (\sin \theta)^2 d \phi (u) d \phi (v)}

Compute the Lagrange equations for motion of a free particle on the sphere and convince yourself that they describe great circles. For example, consider the motion on the equator \displaystyle{\theta = \pi/2} and motion on a line of longitude (\displaystyle{\phi} is constant).

~~~

(define ((Lfree mass) state)
  (* 1/2 mass (square (velocity state))))

(define ((sphere->R3 R) state)
  (let ((q (coordinate state)))
    (let ((theta (ref q 0)) (phi (ref q 1)))
      (up (* R (sin theta) (cos phi))
          (* R (sin theta) (sin phi))
          (* R (cos theta))))))

(define ((F->C F) local)
  (up (time local)
      (F local)
      (+ (((partial 0) F) local)
         (* (((partial 1) F) local)
            (velocity local)))))

(define (Lsphere m R)
  (compose (Lfree m) (F->C (sphere->R3 R))))

(show-expression
 ((Lsphere 'm 'R)
  (up 't
      (up 'theta 'phi)
      (up 'thetadot 'phidot))))

(show-expression
 (((Lagrange-equations
    (Lsphere 'm 'R))
   (up
    (literal-function 'theta)
    (literal-function 'phi)))
  't))

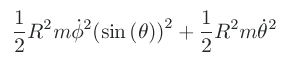
\displaystyle{ \begin{aligned} - \sin \theta (D \phi)^2 \cos \theta + D^2 \theta &= 0 \\ 2 \sin \theta D \theta D \phi \cos \theta + D^2 \phi (\sin \theta)^2 &= 0 \\ \\ D^2 \theta &= (D \phi)^2 \cos \theta \sin \theta \\ D( D \phi (\sin \theta)^2) &= 0 \\ \\ \end{aligned}}

.

So

\displaystyle{ \begin{aligned} D \phi (\sin \theta)^2 &\equiv C \\ \\ \end{aligned}}

for some constant C.

.

Since \displaystyle{ \begin{aligned} D \phi (\sin \theta)^2 &= 0 \\ \\ \end{aligned}} for some \theta,

\displaystyle{ \begin{aligned} D \phi (\sin \theta)^2 &\equiv 0 \\ \\ \end{aligned}}

This is equivalent to setting up the coordinate system such that the initial value of \theta equals zero.

.

Also, since \displaystyle{ \begin{aligned} (\sin \theta)^2 &\ne 0 \\ \\ \end{aligned}} for some \theta,

\displaystyle{ \begin{aligned} D \phi &\equiv 0 \\ \\ \end{aligned}}

.

— Me@2022-10-08 04:56:27 PM

.

.

2022.10.09 Sunday (c) All rights reserved by ACHK

Posted in FDG