守時 6.2

Posted on August 30, 2023 by rpflee

這段改編自 2010 年 4 月 24 日的對話。

通常而言，遲到並非單一事件，而是習慣。背後牽涉了，大量的心結。所以，並不是說他想改，就立刻改到。例如，習慣把超出那一格時段，所能負荷的事件份量，放於時間表的該格之中。

反過來說，如果你遇到一位，「次次也守時」的朋友，他背後一定有，一堆過人之處。生活整體系統而言，運行得不錯。他的優點，絕對不只「守時」一個。

一般人以為，「守時」是一件簡單而容易的事，有心做就會做到。「守時」其實需要刻意經營，成本很高。「守時」既不簡單，亦不容易。

如果你打算「準時」的話，你就會遲到。除了極端巧合的例外，從來只有「早到」或「遲到」，並沒有所謂的「守時」。你要打算「早到」，才有機會「守時」。你願意付出的「早到」時間越多，「守時」的成功機會，就越大。

除了「個別事件要做到守時」的成本很高外，這個難題還有一個，高一個層次的版本：要訓練到一個的人，變到有「守時」的功力，本身的成本亦很高。

— Me@2023-08-29 11:52:56 AM

Euler problem 15.1

Posted on August 27, 2023 by rpflee

— Poorly Drawn Lines

(defun factorial (n)
  (labels
      ((f-iter (m acc)
         (cond ((= m 0) acc)
               ('t (f-iter (1- m)
                           (* m acc))))))
    (f-iter n 1)))

(defun binomial (n r)
  (labels
      ((b-iter (m acc)
         (cond ((< m (1+ (- n r))) acc)
               ('t (b-iter (1- m)
                           (* m acc))))))
    (/ (b-iter n 1) (factorial r))))

— Me@2023-08-26 11:27:59 AM

Ex 1.30 Driven spherical pendulum, 1

Posted on August 23, 2023 by rpflee

Structure and Interpretation of Classical Mechanics

A spherical pendulum is a massive bob, subject to uniform gravity, that may swing in three dimensions, but remains at a given distance from the pivot.

Formulate a Lagrangian for a spherical pendulum, driven by vertical motion of the pivot.

…

~~~

How come [the equations]?

Maybe just using the above equation but set the $r$ constant. But I have
to add a something in order to realize the moving center.

— Me@2006

[guess]

(define (KE-particle m v)
  (* 1/2 m (square v)))

(define ((extract-particle pieces) local i)
  (let* ((indices (apply up
                         (iota pieces
                               (* i pieces))))
         (extract (lambda (tuple)
                    (vector-map
                     (lambda (i) (ref tuple i))
                     indices))))
    (up (time local)
        (extract (coordinate local))
        (extract (velocity local)))))

(define (U-constraint R qs q lambd)
  (* lambd
     (- (square (- q qs))
        (square R))))

(define ((U-gravity g m) q)
  (let ((z (ref q 2)))
    (* m g z)))

(define ((L-rect m R qs U) local)
  (let* ((extract (extract-particle 3))

         (p (extract local 0))
         (t (time p))
         (q (coordinate p))
         (v (velocity p))

         (lambd (ref (coordinate local) 3)))

    (- (KE-particle m v)
       (U q)
       (U-constraint R (qs t) q lambd))))

(let* ((U (U-gravity 'g 'm))
       (xs (lambda (t) 0))
       (ys (lambda (t) 0))
       (zs (literal-function 'z_s))
       (qs (up xs ys zs))
       (L (L-rect 'm 'R qs U))
       (q-rect (up (literal-function 'x)
                   (literal-function 'y)
                   (literal-function 'z)
                   (literal-function 'lambda))))
  (show-expression
   ((compose L (Gamma q-rect)) 't)))

(+ (* (expt R 2) (lambda t))
   (* -1 g m (z t))
   (* 1/2 m (expt ((D x) t) 2))
   (* 1/2 m (expt ((D y) t) 2))
   (* 1/2 m (expt ((D z) t) 2))
   (* -1 (lambda t) (expt (z_s t) 2))
   (* 2 (lambda t) (z_s t) (z t))
   (* -1 (lambda t) (expt (z t) 2))
   (* -1 (lambda t) (expt (y t) 2))
   (* -1 (lambda t) (expt (x t) 2)))

$\displaystyle{ L_r = \frac{1}{2} m \left| \dot {\vec r} (t) \right|^2 - mg z(t) - \lambda(t) \left( \left| \vec r(t) - \vec r_s(t) \right|^2 - R^2 \right) }$

(define ((sf->rf qs) state-with-force)
  (let* ((extract (extract-particle 3))

         (p (extract state-with-force 0))
         (t (time p))
         (q (coordinate p))

         (lambd (ref (coordinate
                      state-with-force) 3))

         (r (ref q 0))
         (theta (ref q 1))
         (phi (ref q 2))

         (xs (ref qs 0))
         (ys (ref qs 1))
         (zs (ref qs 2))

         (x (+ (xs t)
               (* r (sin theta) (cos phi))))
         (y (+ (ys t)
               (* r (sin theta) (sin phi))))
         (z (+ (zs t)
               (* r (cos theta)))))

    (up x y z lambd)))

(let* ((xs (literal-function 'x_s))
       (ys (literal-function 'y_s))
       (zs (literal-function 'z_s))
       (qs (up xs ys zs))
       (q (up (literal-function 'r)
              (literal-function 'theta)
              (literal-function 'phi)
              (literal-function 'lambda))))
  (show-expression
   ((compose (sf->rf qs) (Gamma q))
    't)))

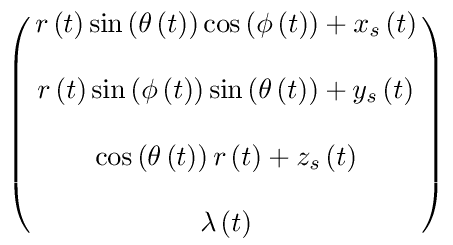
(define ((F->C F) local)
  (->local (time local)
           (F local)
           (+ (((partial 0) F) local)
              (* (((partial 1) F) local)
                 (velocity local)))))

(define (L-driven m R qs U)
  (compose
   (L-rect m R qs U)
   (F->C (sf->rf qs))))

…

[guess]

— Me@2023-08-20 05:02:09 PM

For all, 10.3

Posted on August 16, 2023 by rpflee

Adaptation

No movie can contain all the movies. At least, it cannot contain itself.

— Me@2015-10-10 07:37:26 AM

Self-discovery, 2

Posted on August 16, 2023 by rpflee

The pen is an instrument of discovery rather than just a recording implement.

— Billy Collins

Writing doesn’t just communicate ideas; it generates them.

— Paul Graham

未來騙局, 2

Posted on August 13, 2023 by rpflee

山盟海誓 2.3 | 離婚 3.2.2

這段改編自 2023 年 06 月 20 日的對話。

只有本來，沒有未來。

本來無未來。

承諾皆廢話，未來皆騙局。

除非，那潛在的未來事件，化成了現在，有法律效力的合約，即是未來如果任何一方不遵守，另一方會獲得賠償。亦即是話，所謂的「未來事件」，透過合約，「翻譯」成了現在事件。

「我如今鄭重承認你作我的妻子，並許諾從今以後，無論環境順逆，疾病健康，我將永遠愛慕尊重你，終生不渝。」

— 結婚誓言

「結婚誓言」沒有意思，因為不遵守的話，並沒有任何後果。

承諾 = 騙局

真正有意思的是「離婚協議」，因為它有法律效力，列明了雙方的權利與責任；在婚姻再運行不到時，可立刻啟動操作。

離婚協議，在感情還好時，即是結婚之前，才可以達成。正如人壽保險，在一個人還健康時，才可以買到。

— Me@2023-06-20 12:47:31 PM

Sequential speed

Posted on August 7, 2023 by rpflee

--recurse-paths -r

recurse into directories

--symlinks -y

store symbolic links as the link instead of the referenced file

zip -r -y /dest_folder/the_zip_file.zip /source_folder/

source_folder is the folder to be zipped.

dest_folder is the destination folder for storing the zip file.

After zipping, the resulting file is the_zip_file.zip, which is a zipped version of the source_folder.

— Me@2023-08-03 09:41:29 AM

3.5 Calculating the divergence in higher dimension

Posted on August 2, 2023 by rpflee

A First Course in String Theory

Let $\displaystyle{\vec f = f(r) \hat{\mathbf{r}}}$ be a vector function in $\displaystyle{\mathbb{R}^d}$ .

…

Derive a formula for $\displaystyle{\nabla \cdot \vec f}$ by applying the divergence theorem to a spherical shell of a radius $\displaystyle{r}$ and width $\displaystyle{dr}$ .

…

~~~

Volume and sphere area of an $\displaystyle{n}$ -ball:

$\displaystyle{ \begin{aligned} V_{n}(R)&={\frac {\pi ^{\frac {n}{2}}}{\Gamma \left({\frac {n}{2}}+1\right)}}R^{n} \\ S_{n-1}(R)&={\frac {2\,\pi ^{\frac {n}{2}}}{\Gamma \left({\frac {n}{2}}\right)}}R^{n-1} \end{aligned} \\ }$

Divergence theorem:

$\displaystyle{ \int_V \nabla \cdot \vec f dV = \int_S \vec f \cdot \hat n dS }$

Let $\displaystyle{V}$ be a spherical shell of radius $\displaystyle{r}$ and width $\displaystyle{dr}$ . Then

$\displaystyle{ \begin{aligned} \int_V \nabla \cdot \vec f dV &= \left. \nabla \cdot \vec f \right|_r \int_V dV \\ &= \left. \nabla \cdot \vec f \right|_r \left( S_{n-1}(r) dr \right) \\ \end{aligned} \\ }$

and

$\displaystyle{ \begin{aligned} \int_S \vec f \cdot \hat n dS &= f(r+dr) S_{n-1}(r+dr) - f(r) S_{n-1}(r) \\ \end{aligned} \\ }$

$\displaystyle{ \begin{aligned} \left. \nabla \cdot \vec f \right|_r S_{n-1}(r) dr &= f(r+dr) S_{n-1}(r+dr) - f(r) S_{n-1}(r) \\ \end{aligned} \\ }$

$\displaystyle{ \begin{aligned} \left. \nabla \cdot \vec f \right|_r &= \frac{1}{S_{n-1}(r)} \frac{f(r+dr) S_{n-1}(r+dr) - f(r) S_{n-1}(r)}{dr} \\ &= \frac{1}{S_{n-1}(r)} \frac{d}{dr} \bigg( f(r) S_{n-1}(r) \bigg) \\ &= \frac{1}{r^{n-1}} \frac{d}{dr} \bigg( r^{n-1} f(r) \bigg) \\ \end{aligned} \\ }$

— Me@2023-08-02 09:28:32 AM

For all, 10.2

Posted on August 1, 2023 by rpflee

Adaptation

No movie can record its whole “the making of”.

Even two mutual movies [that record each other’s “the making of”] cannot work around this.

— Me@2015-10-19 06:13:58 PM

Physics Town

continues

Monthly Archives: August 2023