p_27 = -(2 * a - 1) * (a ^ 2 - a + 41)
where
n = 1000
m = head $ filter (\x -> x ^ 2 - x + 41 > n) [1 ..]
a = m - 1
Euler Problem 27 asks us to find a quadratic equation of the form  that generates the most consecutive prime numbers starting from
that generates the most consecutive prime numbers starting from  , with the constraints
, with the constraints  and
and  . The final answer is the product
. The final answer is the product  for the winning pair. The “official” Haskell solution looks cryptic, but there’s a clever trick behind it. Let’s break it down step-by-step in a way that’s easier to follow.
for the winning pair. The “official” Haskell solution looks cryptic, but there’s a clever trick behind it. Let’s break it down step-by-step in a way that’s easier to follow.
A Handy Math Trick: Shifting the Quadratic
Imagine we tweak our quadratic  by replacing
by replacing 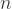 with
with  . When we expand it out, we get:
. When we expand it out, we get:

This is still a quadratic in 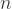 , but now the coefficients are:
, but now the coefficients are:
By choosing the right  , we can transform any quadratic into a simpler form, like
, we can transform any quadratic into a simpler form, like  or
or  . This is our starting point.
. This is our starting point.

Which Form Works Best?
- Form 1:

This one’s a dud. Plug in  , and you’ll see every other number is even (e.g.,
, and you’ll see every other number is even (e.g.,  ). With so many evens, it can’t produce a long run of primes—primes are mostly odd (except 2).
). With so many evens, it can’t produce a long run of primes—primes are mostly odd (except 2).
- Form 2:

This is more promising. A mathematician named Rabinowitz proved that for this form to generate the longest sequence of primes,  must be a special number called a Heegner number. There are only six possibilities, and after testing,
must be a special number called a Heegner number. There are only six possibilities, and after testing,  comes out on top. It spits out 40 primes from
comes out on top. It spits out 40 primes from  to
to  . The runner-up,
. The runner-up,  , doesn’t do as well.
, doesn’t do as well.
So,  is our golden ticket. But there’s more to it.
is our golden ticket. But there’s more to it.
The Symmetry Bonus
Here’s a cool trick with  :
:

This means if  gives a prime (like 47), then
gives a prime (like 47), then  (i.e.,
(i.e.,  ) does too (also 47). The sequence works both ways—positive and negative
) does too (also 47). The sequence works both ways—positive and negative 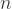 . Starting at
. Starting at  , we get 40 primes up to
, we get 40 primes up to  , but we can also count backward with negative
, but we can also count backward with negative 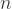 . Our goal is to shift this quadratic so we capture more of these primes from
. Our goal is to shift this quadratic so we capture more of these primes from  onward, while keeping
onward, while keeping  and
and  within the problem’s limits.
within the problem’s limits.

Fitting It Into the Rules
Let’s start with  (where
(where  ) and shift it using our trick:
) and shift it using our trick:
The problem says  and
and  , so:
, so:
The second condition is trickier because  grows fast. We need the biggest
grows fast. We need the biggest  where
where  .
.

Crunching the Numbers
Let’s test some  values:
values:
 :
:  (under 1000)
(under 1000) :
:  (over 1000)
(over 1000)
So,  is the largest value that works. Now calculate:
is the largest value that works. Now calculate:

 (from above)
(from above)
Check the constraints:
 ✓
✓ ✓
✓

The Haskell Code Explained
That’s where this funky code comes in:
n = 1000
m = head $ filter (\x -> x ^ 2 - x + 41 > n) [1 ..]
a = m - 1
It finds  (first
(first  where
where  ). Then
). Then  .
.
The final line:
p_27 = -(2 * a - 1) * (a ^ 2 - a + 41)
This is a bit off. It uses  , but we need
, but we need  . The correct product should be:
. The correct product should be:
The code’s formula seems to be a typo or a leftover from a different derivation. It should just compute  .
.

Why It Works
With  , the quadratic
, the quadratic  generates 71 primes from
generates 71 primes from  to
to  . This shift captures more of the
. This shift captures more of the  sequence’s primes in the positive direction, thanks to the negative
sequence’s primes in the positive direction, thanks to the negative  . The product -59231 is the answer.
. The product -59231 is the answer.
Wrapping Up
This solution is sneaky—it starts with a prime-generating champ, shifts it just right, and fits the problem’s rules. It’s not the brute-force way (testing every  and
and  ), but a math shortcut that lands on the perfect answer. Pretty cool, right?
), but a math shortcut that lands on the perfect answer. Pretty cool, right?
— Me@2025-03-24 12:25:20 PM
.
.
2025.03.30 Sunday (c) All rights reserved by ACHK























You must be logged in to post a comment.