Pure Maths 6
Past papers 20
這段改篇自 2010 年 2 月 7 日的對話。
… 無限個的是 S = a/(1-r) … 有限個的是 … 我不是太記得 … 好像是 S = a(1-r^n)/(1-r)。對不對?
(LWT:不記得。)
你竟然不記得。那真是要把這公式記在你的 Tip Paper(精讀筆記)中。你連 Form 5(中學五年級,會考)的東西也不記得。那會構成很太問題。
(LWT:那些 Form 5 時學過的東西,過了暑假以後,很多科也是這樣,我也好像忘記掉了。)
不會的。首先,你要知道一點:輸入了腦中的東西,就永遠存在,不會消失。[1] 這一點接不接受到?
(LWT:就算東西仍然存在於腦海中,人有時會不記得的。)
你要分清楚。例如,你想不起資料 A。你要分清楚究竟是
1. 從來沒有 A(輸入過腦海中),還是
2. 有 A(輸入過腦海中),只是不記得。
那是兩回事。
(LWT:總之輸入過,就會永遠在腦海中?)
輸入過,就會永遠在腦海。我們「忘記」事件,並不是因為腦海中的記憶消失了,而是因為腦海中的記憶沒有被整理過,太多太混亂,導致不能有效率地把提取需要的資料。
「忘記了輸入過的東西」和「腦海中從來也沒有那樣東西」,是兩回事。太部分人以為「忘記了某樣東西」,等如「那樣東西從腦海中消失了」。那是錯的。明不明白?
(LWT:明白。)
輸入過腦海的東西,即是「已經有」的東西,可以很快地 reload(重新裝載)出來,因為那些是「已經有」的東西,而不是「新學」的東西。
(LWT:那我需不需要刻意去溫習 Form 5 的東西?)
那其實就很簡單:Form 5 的課程內容當中,與 Form 6 有關的東西就刻意去記。其餘的,就毋須刻意花時間去溫習。
那你怎樣知道什麼東西「與 Form 6 有關」呢?
例如,你今次是因為忘記了 S = a/(1-r) 和 S = a(1-r^n)/(1-r),而不能完成這一題。你就應該立刻把這兩句公式,記在你的 Tip Paper 中。那就已經足夠。千萬不要過份認真,拿回 Form 5 的數學書慢慢研究。那會做成鉅大的時間浪費。
(LWT:但是很多 Form 5 AMaths(Additional Mathematics 附加數學)的公式,我都用不回出來(,不能有效運用)。)
重點是,會不會因為不用那些 Form 5 AMaths 的公式,而影響你的 ALevel Pure Maths(高考,純數學)的成績呢?
如果你不運用 Form 5 AMaths 的公式,也不會影響 Pure Maths 的成績的話,那就不用理會它。如是有影響的話,你會在平日做 Pure Maths 題目和 past papers(歷屆試題)時,發現到的。那你就立刻把那些 Pure Maths 所需的 Form 5 AMaths 公式,記在你的 Tip Paper 中。
用這類方法,就可以很有效率地 reload 以前學過的東西。
— Me@2010.04.22
[1] 這句並不是百分百準確的科學事實,但是可信可用。
2010.04.22 Thursday (c) All rights reserved by ACHK
的意思是「電線越長,電阻就越大」和「電線越粗,電阻就越小」。如果你記得物理意義的話,你就根本不可能將分子分母錯誤地倒轉。

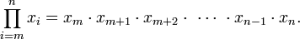
You must be logged in to post a comment.