（反對）開夜車 4.2

Posted on August 3, 2019 by rpflee

…

平均而言，你仍必須要有，充足的睡眠。亦即是話，某一天睡少了，就必須於在當個星期，還回「睡債」。

例如，如果你的充足睡眠是，每天七小時，而你在某一天只睡了六小時的話，你就有義務，在當個星期的另一天，睡多一小時。一般而言，「另一天」是指週末，或者其他假日。

另外，有時，只要跳出框框，破格思考，你會發現，或者，只要你的時間表稍改一點，就根本毋須「開夜車」。

例如，我在大學一年級時，發覺日間的課堂，加課外活動，異常充實。回到家時，就已經累到，根本集中不到精神研習。

我當時靈機一觸想到，與其沒有精神地研習，倒不如每晚九時半就睡，凌晨三或四時才起床。那樣，七時多出門前，我就會有，三至四個小時的專心時空。

— Me@2019-07-30 11:11:42 PM

（反對）開夜車 4.1

Posted on June 8, 2019 by rpflee

本文章並(!)不(!)可作為醫學建議。如需醫學意見，請諮詢專業人士。

（問：但是，在現今社會，無論是上班，或是讀書，完全不「開夜車」，又好像不切實際。）

其實，主要是講讀書時代。如果在工作時代，你的職位需要，你時常「開夜車」的話，你根本就應該另謀高就。

試問，世間上，有什麼工作，竟然值得你冒生命危險，去時常「開夜車」呢？

言歸正傳，讀書時代，如果時間管理得宜，需要「開夜車」的情況，其實是很少。

（問：那樣說有意思嗎？我正正是問你，在時間管理失宜，需要「開夜車」時，該如何自處？）

一定「開夜車」的話，你至少要做到以下幾點，去保障自己的安全：

只可以間中，不可以經常。
日間中途要有小睡。
平均而言，你仍必須要有，充足的睡眠。亦即是話，某一天睡少了，必須於在當個星期，還回「睡債」。
- 例如，如果你的充足睡眠是，每天七小時，而你在某一天只睡了六小時的話，你就有義務，在當個星期的另一天，睡多一小時。

另外，有時，只要跳出框框，破格思考，或者，只要你的時間表稍改一點，就根本毋須「開夜車」。

本文章並(!)不(!)可作為醫學建議。如需醫學意見，請諮詢專業人士。

— Me@2019-06-06 08:23:56 PM

追憶逝水年華, 3

Posted on May 10, 2019 by rpflee

In Search of Lost Time, 3 | （反對）開夜車 3.1 | 止蝕 4

其實，我中五那年，試過企圖「開夜車」。詳細過程怎樣，已不太記得。但是，總體的感受，仍然是深刻。

那時，我有很多天真的想法，例如：

~~1. 只要每晚睡少四小時，就每晚可以多四小時溫習。~~

~~2. 只要每晚可以多四小時溫習，就可以追回之前，落後了的進度。~~

實情是，「貪心」帶來「貧窮」：

很多時，我也是覺得自己，溫習的進度落後了，來不及準備那年的公開試。所以，想透過凌晨（例如）三時起牀，來追回之前，落後了的進度。但是，我卻幾乎每天凌晨，也起不到牀，導致溫習大計失敗，遺撼非常。繼而，因為失落了，更多的時間，我就覺得，更加需要在下一天，凌晨起牀。

惡性循環，持續了很久，浪費了我大量的時間。其實，只要我睡眠適量，作息定時，反而有不少機會，有上佳的成績。

現在回想起來，仍然驚嘆著，為何年輕時，可以那麼愚蠢。

只可以說，人在惶恐時，多麼糊塗的事，都可以發生。

— Me@2019-05-09 10:04:55 PM

（反對）開夜車 2.5

Posted on April 16, 2019 by rpflee

本文章並(!)不(!)可作為醫學建議。如需醫學意見，請諮詢專業人士。

…

（問：「只要飛蚊不惡化」？你怎能保證？）

不能。那正正就是，我更大的苦惱。

一日不能知道，我當年開始患飛蚊症的真正原因，我也會不安，擔心症狀加劇。

「飛蚊症」只是某個或某些疾病的一個「症」，而不是「疾病」本身。一日不能知道，我飛蚊症的病因，我也不能有力預防，症狀的加劇。

（問：你不是說，長期夜睡少睡，導致你的飛蚊症嗎？）

那只是估計，不是肯定。

那一段時間，「出事」前的一兩個星期，我剛好時常睡不著，導致睡了很少。所以，長期夜睡少睡，很可能是主要的原因。

當然，如果平日的睡眠充足，並不會因為單一事件，某一晚的夜睡少睡，就立刻有飛蚊。如果人體是那麼沒有彈性，人類這種生物，可能一早就已經絕種了。

但是，如果是長期夜睡少睡，身體自然會越來越虛弱。到達某個臨界點時，意外事件就可以隨時發生。從相反的角度來講，如果平日睡眠適量，就等於刪除了，飛蚊症的其中一個主要誘因，從而大大減低了，其發生的機會率。

本文章並(!)不(!)可作為醫學建議。如需醫學意見，請諮詢專業人士。

— Me@2019-04-13 03:34:33 PM

（反對）開夜車 2.4

Posted on March 19, 2019 by rpflee

本文章並(!)不(!)可作為醫學建議。如需專業意見，請諮詢專業人士。

…

至於，我自己的案例，則幸好是良性的，不會致盲；只要飛蚊不惡化，視力不會減弱。

（問：但你剛才說，飛蚊症「會帶來精神困擾」？）

無錯。可以說是心靈創傷。

（問：為什麼呢？）

如果你買了一個電腦熒光幕，發現有死點，你會怎樣做？

（問：立刻要求商戶更換。新買的電器，必定在保養期內，可以更換。）

假設不可更換呢？

（問：如果只是一兩點的話，應該不會太明顯。我會先用它，直到幾年後才再換。

但是，如果不只是一兩點的話，我可能會忍受不到；如果我負擔得起，我會立刻買過另一部。）

再假設，你永久不能更換熒光幕呢？

（問：永久有死點？）

無錯。

（問：那又真的，十分不自在。

你的意思是，「熒光幕永久有死點」就是患飛蚊症的感受？）

無錯。

所以，患了飛蚊症以後，我一聽到「不可逆轉」這四個字，就有一點兒緊張；患了飛蚊症以後，我以為，我人生不可能再快樂。

幸好，一年之後，我竟然習慣了——只要飛蚊不惡化，我就不會因為那些「死點」，而明顯不開心。

（問：「只要飛蚊不惡化」？你怎能保證？）

不能。那正正就是，我更大的苦惱。

一日不能知道，我當年開始患飛蚊症的真正原因，我也會不安，擔心症狀加劇。

「飛蚊症」只是某個或某些疾病的一個「症」，而不是「疾病」本身。一日不能知道，我的飛蚊症的病因，我也不能有力預防，症狀的加劇。

（問：你不是說，長期夜睡少睡，導致你的飛蚊症嗎？）

…

本文章並(!)不(!)可作為醫學建議。如需專業意見，請諮詢專業人士。

— Me@2019-03-18 04:47:58 PM

（反對）開夜車 2.3

Posted on February 26, 2019 by rpflee

Ken Chan 時光機 1.4.2.3

本文章並(!)不(!)可作為醫學建議。如需專業意見，請諮詢專業人士。

…

結果，他那天只睡了，一個半小時。

我那時以為，那沒有什麼大不了。但是現在，我也已一把年紀了，才驚覺，只要有一點不幸，那就可以造成，嚴重的後果。

（問：那有什麼「嚴重的後果」？）

「嚴重後果」中，較為輕微的，我也經歷過，而且可以視為「不可逆轉」的。

例如，大前年開始，我左眼患有飛蚊症。即是話，視野中，有一些黑點等，不應存在的小垃圾。

飛蚊症可以視為「不可逆轉」的原因是，以現今科技，醫治飛蚊症方法，風險遠比「良性飛蚊」的症狀本身高。所以，除非一個人的飛蚊症極度嚴重，否則，眼科醫生也不會建議病人，去接受那些手術。

（問：「良性飛蚊」？）

「良性飛蚊」的「良性」，並不是說真的有益，而只是指「不會致盲，只會帶來精神困擾」。

至於「惡性飛蚊」，即是指「有致盲風險」，因為，那代表著，視網膜開始脫落；必須立刻做手術制止之。

(問：如果開始有飛蚊，自己又怎會知道是，「良性」還是「惡性」呢？）

不會知道。

所以：

第一，你要在未有飛蚊時，防範於未然。
第二，萬一仍然出現飛蚊的話，要立刻看眼科醫生，讓他為你檢查，是否視網膜開始脫落。
- 如果不是，就不用擔心。
- 如果是，可以立刻做手術，制止視網膜脫落，保住完整的視力。視網膜開始脫落，而不立刻做手術制止之，有致盲的風險。

至於，我自己的案例，則幸好是良性的，不會致盲；只要飛蚊不惡化，視力不會減弱。

（問：但你剛才說，飛蚊症「會帶來精神困擾」？）

無錯。可以說是心靈創傷。

（問：為什麼呢？）

…

本文章並(!)不(!)可作為醫學建議。如需專業意見，請諮詢專業人士。

— Me@2019-02-25 04:01:37 PM

（反對）開夜車 2.2

Posted on February 3, 2019 by rpflee

Ken Chan 時光機 1.4.2.2

The light that burns twice as bright burns half as long, …

— Blade Runner (1982)

…

可能，因為他「溫習到凌晨」式的方法，對他來說有效，他亦鼓勵學生那樣做。

我現在的記憶，暫時未能確定，他在課堂中，有沒有明示推介過，用這個方法。但是，我記得在他派發的筆記中，其中一頁，有一個正在深夜讀書的漫畫。而在漫畫下面，有一句「study to 3 a.m.」（讀書至深夜三點鐘）。

長話短說，我是反對這個方法的，理由有很多，例如：

第一，長期睡眠不足，會導致腦袋呆了，大大減低下一天的工作效率。

第二，長期睡眠不足，會導致身體時常病。

在 Ken Chan 的部分課堂，特別是假期的補課中，我就見到他時常咳嗽。可能，他在工作時代，仍然過著，極度忙碌的生活。

還記得在九月，在課程的第一課，他就已經遲到，遲了大概 15 至 30 分鐘之間。那課原定於早上八時半開始。上課中途，他有點咳嗽。他說，因為當天早上之前，吸入了太多的氮氣。他懷疑一位同事，作弄了他。

話說，他工作的地方，有一部儀器壞了。他的同事跟他說：「部機好似壞咗，漏緊啲 nitrogen 喎，你聞下係唔係？」（那儀器疑似壞了，正在洩漏氮氣。你聞一聞，看看是不是。）

Ken Chan 事後回心一想，才醒起：「Nitrogen 又點會有味咖？」（氮氣又何來會有味道呢？）

結果，他那天只睡了，一個半小時。

我那時以為，那沒有什麼大不了。但是現在，我也已一把年紀了，才驚覺，只要有一點不幸，那就可以造成，嚴重的後果。

— Me@2019-02-03 07:02:42 AM

（反對）開夜車 2.1

Posted on January 19, 2019 by rpflee

Ken Chan 時光機 1.4.2.1

之前提到，Ken Chan 所讀的中學不正常：

「

在中四和中五的校內考試測驗中，不斷地考核高考課程。所以，他在中四時代開始，已經要鑽研，高考程度和大學程度的物理。

」

那樣，他何來有，那麼多的時間呢？

那時，他往往要讀書，至通宵達旦。

那樣，他的公開試成績，又如何呢？

根據他所講，他事後發現，會考物理科中的 MC（多項選擇題）部分，錯了兩題；他達不到他原本,「全部科目全部滿分」的理想。

那樣，他又做不做到「狀元」，全部科目「奪 A」呢？

他在另一天的課堂中，暗示自己當年，差一點才做到「狀元」：

（我暫時不記得，他以下說話的上半句是什麼。）

「

… 如何不是那樣，我就毋須於，放榜當天的晚上，在家裡哭。唉！還是不說了。

」

當時，我想知道詳情。可惜，他真的沒有說下去，我也沒有辦法。

雖然，主觀而言，從他自己的角度，成績不是理想，因為，那不是「全部科目全部滿分」；但是，如果不是對自己，那麼苛刻的話，客觀來說，他的成績是上乘的。

可能，因為他「溫習到凌晨」式的方法，對他來說有效，他亦鼓勵學生那樣做。

長話短說，我是反對這個方法的，…

— Me@2019-01-18 03:47:50 PM

Ken Chan 時光機 2.2

Posted on January 6, 2019 by rpflee

聖誕假後的常規課程中，Ken Chan 預計應該不會有時間，教光學和熱學。但是，他認為那兩個課題很淺易，所以，期望我們即使自修，也沒什麼難度。

但是，他後來改變主意，還是決定於，農歷新年的年初一、二、三，為我們補課，教回光學和熱學。

今次，那三天的課，他不單不收我們的學費，他還要自己，花時間找課室、花金錢付租金。

後來，他改為每天收 20 元，即是總共 60 元。他解釋道，補課社的職員因為他的補課，要犧牲那三天的農曆新年假期。那每人 60 元的學費是，全數慰勞他們的。

那三天的補課，好處是光學和熱學；壞處是，由於每天也補多個小時，我少了大量，各科的溫習時間。但是，那個農曆新年長假，因為我自己時間管理不善，而損失的時間，遠多於那三天的補課時間。

感謝 Ken Chan 的額外付出。我亦慶幸，生於那個時空，還是有真人授課的年代。出生遲十年，就已經只能透過錄影帶，來獲得 Ken Chan 的教導。

— Me@2019-01-06 02:18:47 PM

Ken Chan 時光機 2.1

Posted on December 27, 2018 by rpflee

當年是 1996 年，我 9 月開始上他的課程。每星期上 1.5 小時，由星期六早上 8 時半，上到 10 時正。所以，每個星期六，我也要在還未睡夠時，就很早起床。去補習社的路程中，往往是一邊行，一邊流鼻水；唯有勉勵自己：「即使再辛苦，只要捱過『會考』（公開試），就可以有好日子過。」

記憶所及，大概在聖誕前，剛好完成了力學分部。

然後，他於聖誕假期中，有額外補課—歷時三天的全日課程，不再是每天 1.5 小時。就在那三天，他要完成波動分部。

他在公佈有這個聖誕波動補課時，我有兩點不開心。

第一點是，我要交額外的學費。不過，相對於第二點而言，那也只是小問題。

第二點是，那補課的學額有限，只有常規課程的兩成。我現在的記憶可能有誤，未必真的是兩成，但也必定是，遠少於他常規課程的學生數目。換句話說，如果供不應求，我就可能報讀不到。幸好，正正是因為這個擔憂，我及早報名，爭取到一個補課學位。

— Me@2018-12-27 03:50:13 PM

迷宮直升機 5.3

Posted on December 17, 2018 by rpflee

Ken Chan 時光機 1.4.3

…

其實，那種情形，對現為中四的你而言，並不只是一個「假設」，因為，你現正修讀， G.Maths（核心數學）和 A.Maths（附加數學）。

「附加數」比「基礎數」而言，艱深非常，大部分人也覺得，十分辛苦。但是，亦正正是因為「附加數艱深非常」，你才會覺得「核心數容易萬分」。

那又為什麼，會有這個現象呢？

（問：程度高了？）

無錯。水平高了。

試想想，你參加了一個走迷宮比賽—與另外幾位參賽者，鬥快逃出同一個迷宮。

在那個情況下，「勤力」一點，跑快一些，是沒有什麼大作用的；因為，你只要在其中一個分岔路口，做錯決定，你就已經可以，前功盡廢。

走迷宮的致勝之道—在現埸極速逃出的方法是，在事前用大量時間準備，一架直升機，在比賽期間，把你釣出迷宮。

即使沒有那麼多資源，至起碼，在比賽開始前，你就要準備好，該迷宮的平面圖。

（問：無論是直升機，或者是鳥瞰圖，好像都是犯規？）

那要視乎，具體是哪一個遊戲。

試想想，中學生自修大學程度的課程，有沒有犯規？

（問：似乎沒有。但是，那又好像十分辛苦。）

一般而言，世間少有不勞而獲的東西。鉅大的好處，很多時也需要付出，鉅大的代價。

還有，如果策略妥當，閱讀大學程度書籍，所需的額外時間，未必如想像中的那麼多。

比喻說，假設你修讀 A.Maths（附加數學）的唯一目的是，提升 G.Maths（核心數學）。那樣，你的「附加數」成績，並不需要保證，名列前茅。

反而，即使在最壞情況，你的「附加數」成績不合格，只要你曾經用心研習過，「附加數」也會令你覺得，「核心數」容易了很多。

同理，如果你閱讀大學物理書籍的主要目的是，提升中學物理的話，你並不需要完成，整本「大學物理」的課文和習題。

反而，最重要的是，你嘗試過「大學物理」中，部分題目的難度；那就足以令你感到，中學的版本，顯淺非常。

— Me@2018-12-17 07:05:34 PM

迷宮直昇機 5.2

Posted on December 9, 2018 by rpflee

Ken Chan 時光機 1.4.2

…

但是，他的學校不正常——在中四和中五的校內考試測驗中，不斷地考核高考課程。所以，他在中四時代開始，已經要鑽研，高考程度和大學程度的物理。

結果，到真正會考時，由於「只會」考核中五程度的東西，他會突然覺得十分容易。

其實，那種快感不難體會。

假設，你現在是中學四年級。

你想像，如果突然之間，那份中四的數學卷，換成中一程度的數學卷。你會有什麼感受？

你不單會覺得如釋重負，而且會有信心，有機會取滿分；即使，那份中一測驗卷的課題，在中一以後，從來未刻意溫習過。

（問：我又不敢說，我一定會滿分。）

我沒有說「一定」。我只是說「覺得有機會」。

試想想，現為中四的你，面對一份中四的數學卷，你夠不夠膽說「有機會取滿分」？

（問：不太敢，因為，那幾乎沒有可能。但是，我明白你的意思。現在要我做回中一的測驗卷，又真的會覺得，一定會高分，可能會滿分。）

其實，那種情形，對現為中四的你而言，並不只是一個「假設」，因為，你現正修讀， G.Maths（核心數學）和 A.Maths（附加數學）。

「附加數」比「基礎數」而言，艱深非常，大部分人也覺得十分辛苦。但是，亦正正是因為「附加數艱深非常」，你才會覺得「核心數容易萬分」。

那又為什麼，會有這個現象呢？

— Me@2018-12-09 09:03:02 PM

Ken Chan 時光機 1.4.1

Posted on November 18, 2018 by rpflee

迷宮直昇機 5.1

…

至於第三個技巧，則實在是最宏觀，亦可能是最重要。

Ken Chan 說：「你們現在會盤算，在會考中，各科太概會有什麼目標，奪取什麼等級的成績。但是，我當年全部科目，只有一個目標，就是要『攞 full』」。

那就即是要，全部科目中的每一科，不只要甲等，而是要滿分；因為在當年，如果可以在全部科目奪得滿分，考生會獲頒一張特別證書。他那時就為了，那張證書而努力。

但是，那是如何辦到的呢？

考生在中五時參加「會考」，中七時參加「高考」。所以，正常的學校，會在中四和中五的校內考試測驗中，考核會考課程。

結果，到真正會考時，由於「只會」考核中五程度的東西，他會突然覺得十分容易。

— Me@2018-11-18 10:06:43 PM

Ken Chan 時光機 1.3

Posted on October 31, 2018 by rpflee

唔識就飛 8.4.2

…

另一個技巧是，考試時「唔識就飛」：想不通的話，就立刻先做下一題，或者同一題的下一部分。

假設我現時記憶正確，Ken Chan 是第一個教我這個技巧的老師；我日校的純數學科老師，則是第二個（亦是最後一個）。

這個技巧，對我來說，實在太重要，因為，在兩年多後的純數學科高考中，如果我不是確切執行這個政策的話，我有極大機會會失手，繼而在當年，升不到大學。

那個故事，現不再詳述，因為已於另一篇文章「唔識就飛 8.4」中講過。請參考該文章。

— Me@2018-10-31 09:39:05 AM

如有 HKDSE physics 香港中學文憑試之物理問題，歡迎以右邊之電郵地址，聯絡本人。

Ken Chan 時光機 1.2

Posted on October 20, 2018 by rpflee

多項選擇題 7.2 | Multiple Choices 7.2

…

重點是，無論「勤力」還是「懶惰」，也只是手段，不是目的本身。

二來，即使有時，「勤力」是正確的；那又應該如何「勤力」呢？

我的老師中，大概只有兩位，曾經講過一點讀書方法。其中一位，就正正是 Ken Chan。（另一位則是，我日校的「純數學」的老師（程兆海）。）

我記憶所及，Ken Chan 教過的溫習技巧，又不是真的很多，因為他並沒有，（例如）花一個課堂的時間去講。但是，就憑他有講的一點點，就已經令我，受用無窮。

Ken Chan 所提及，其中一個技巧是，在物理科，如果新學一個課題，就應該先做，大量該個課題的 MC（多項選擇題）。那樣，你就可以極速釐清，該個課題中的新概念。

註：必須為考試局所出的，以往公開試題目，而不是坊間出版社的練習。

— Me@2018-10-20 11:46:04 AM

如果需要聯絡本人，可用右邊的電郵地址。

Ken Chan 時光機 1.1

Posted on October 5, 2018 by rpflee

多項選擇題 7 | Multiple Choices 7

我在中學時代，很想知道讀書方法。但來，近乎從來沒有老師，教授求學攻略；彷彿那完全不重要。

大部分老師，大概只會說：「勤力一點。」

那是答非所問。

一來，勤力一定有用嗎？

如要只要勤力，就解決到問題的話，世界會簡單很多。實情是，那不會。

試想想，人的科技發展幅度，遠大於其他動物，並不是因為人勤力過其他動物。有時候，剛剛相反。正正是因為人想「偷懶」，才會發展各式各樣的科技，以逸代勞。

重點是，無論「勤力」還是「懶惰」，也只是手段，不是目的本身。

— Me@2018-10-03 03:59:04 PM

如果需要聯絡本人，可用右邊的電郵地址。

The Jacobian of the inverse of a transformation

Posted on August 9, 2018 by rpflee

The Jacobian of the inverse of a transformation is the inverse of the Jacobian of that transformation

In this post, we would like to illustrate the meaning of

the Jacobian of the inverse of a transformation = the inverse of the Jacobian of that transformation

by proving a special case.

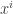Consider a transformation $\mathscr{T}: \bar{x}^i=\bar{x}^i (x^1,x^2)$ , which is an one-to-one mapping from unbarred $x^i$ ‘s to barred $\bar{x}^i$ coordinates, where $i=1, 2$ .

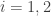By definition, the Jacobian matrix J of $\mathscr{T}$ is

$J= \begin{pmatrix} \displaystyle{\frac{\partial \bar{x}^1}{\partial x^1}} & \displaystyle{\frac{\partial \bar{x}^1}{\partial x^2}} \\ \displaystyle{\frac{\partial \bar{x}^2}{\partial x^1}} & \displaystyle{\frac{\partial \bar{x}^2}{\partial x^2}} \end{pmatrix}$

Now we consider the the inverse of the transformation $\mathscr{T}$ :

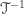$\mathscr{T}^{-1}: x^i=x^i(\bar{x}^1,\bar{x}^2)$

By definition, the Jacobian matrix $\bar{J}$ of this inverse transformation, $\mathscr{T}^{-1}$ , is

$\bar{J}= \begin{pmatrix} \displaystyle{\frac{\partial x^1}{\partial \bar{x}^1}} & \displaystyle{\frac{\partial x^1}{\partial \bar{x}^2}} \\ \displaystyle{\frac{\partial x^2}{\partial \bar{x}^1}} & \displaystyle{\frac{\partial x^2}{\partial \bar{x}^2}} \end{pmatrix}$

On the other hand, the inverse of Jacobian $J$ of the original transformation $\mathscr{T}$ is

$J^{-1}=\displaystyle{\frac{1}{ \begin{vmatrix} \displaystyle{\frac{\partial \bar{x}^1}{\partial x^1}} & \displaystyle{\frac{\partial \bar{x}^1}{\partial x^2}} \\ \displaystyle{\frac{\partial \bar{x}^2}{\partial x^1}} & \displaystyle{\frac{\partial \bar{x}^2}{\partial x^2}} \end{vmatrix} }} \begin{pmatrix} \displaystyle{\frac{\partial \bar{x}^2}{\partial x^2}} & \displaystyle{-\frac{\partial \bar{x}^1}{\partial x^2}} \\ \displaystyle{-\frac{\partial \bar{x}^2}{\partial x^1}} & \displaystyle{\frac{\partial \bar{x}^1}{\partial x^1}} \end{pmatrix}$

If $\bar{J} = J^{-1}$ , their (1, 1)-elementd should be equation:

$\displaystyle{\frac{\partial x^1}{\partial \bar{x}^1}}\stackrel{?}{=}\displaystyle{\frac{1}{\displaystyle{\frac{\partial \bar{x}^1}{\partial x^1}}\displaystyle{\frac{\partial \bar{x}^2}{\partial x^2}}-\displaystyle{\frac{\partial \bar{x}^1}{\partial x^2}}\displaystyle{\frac{\partial \bar{x}^2}{\partial x^1}} }} \bigg( \displaystyle{\frac{\partial \bar{x}^2}{\partial x^2}} \bigg)$

Let’s try to prove that.

Consider equations

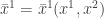
$\bar{x}^1 = \bar{x}^1(x^1,x^2)$

$\bar{x}^2 = \bar{x}^2(x^1,x^2)$

Differentiate both sides of each equation with respect to 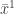$\bar{x}^1$ , we have:

$A := 1=\displaystyle{\frac{\partial \bar{x}^1}{\partial \bar{x}^1}=\frac{\partial \bar{x}^1}{\partial x^1}\frac{\partial x^1}{\partial \bar{x}^1}+\frac{\partial \bar{x}^1}{\partial x^2}\frac{\partial x^2}{\partial \bar{x}^1}}$

$B := 0 = \displaystyle{\frac{\partial \bar{x}^2}{\partial \bar{x}^1}=\frac{\partial \bar{x}^2}{\partial x^1}\frac{\partial x^1}{\partial \bar{x}^1}+\frac{\partial \bar{x}^2}{\partial x^2}\frac{\partial x^2}{\partial \bar{x}^1}}$

$A \times \displaystyle{\frac{\partial \bar{x}^2}{\partial x^2}}:~~~~~C := \displaystyle{\frac{\partial \bar{x}^2}{\partial x^2}=\frac{\partial \bar{x}^1}{\partial x^1}\frac{\partial x^1}{\partial \bar{x}^1}\frac{\partial \bar{x}^2}{\partial x^2}+\frac{\partial \bar{x}^1}{\partial x^2}\frac{\partial x^2}{\partial \bar{x}^1}\frac{\partial \bar{x}^2}{\partial x^2}}$

$B \times \displaystyle{\frac{\partial \bar{x}^1}{\partial x^2}}:~~~~~D := \displaystyle{0=\frac{\partial \bar{x}^2}{\partial x^1}\frac{\partial x^1}{\partial \bar{x}^1}\frac{\partial \bar{x}^1}{\partial x^2}+\frac{\partial \bar{x}^2}{\partial x^2}\frac{\partial x^2}{\partial \bar{x}^1}\frac{\partial \bar{x}^1}{\partial x^2}}$

$D-C:$

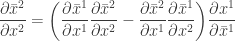$\displaystyle{ \frac{\partial \bar{x}^2}{\partial x^2}= \bigg( \frac{\partial \bar{x}^1}{\partial x^1}\frac{\partial \bar{x}^2}{\partial x^2} - \frac{\partial \bar{x}^2}{\partial x^1}\frac{\partial \bar{x}^1}{\partial x^2}\bigg) \frac{\partial x^1}{\partial \bar{x}^1}}$ ,

results

$\displaystyle{ \frac{\partial x^1}{\partial \bar{x}^1}}=\frac{\displaystyle{\frac{\partial \bar{x}^2}{\partial x^2}}}{\displaystyle{\frac{\partial \bar{x}^1}{\partial x^1}\frac{\partial \bar{x}^2}{\partial x^2} - \frac{\partial \bar{x}^1}{\partial x^2}\frac{\partial \bar{x}^2}{\partial x^1}}}$

…

— Me@2018-08-09 09:49:51 PM

Chain Rule of Differentiation

Posted on July 15, 2018 by rpflee

Consider the curve $y = f(x)$ .

$\displaystyle{\frac{d}{dx}}$ is an operator, meaning “the slope of the tangent of”. So the expression $\displaystyle{\frac{dy}{dx}}$ , meaning $\displaystyle{\frac{d}{dx} (y)}$ , is not a fraction.

In order words, it means the slope of the tangent of the curve $y = f(x)$ at a point, such as point $A$ in the graph.

d_2018_07_15__21_31_32_PM_

The symbol $dx$ has no relation with the symbol $\displaystyle{\frac{dy}{dx}}$ . It means $\Delta x$ as shown in the graph. In other words,

$dx = \Delta x$

The symbol $dy$ also has no relation with the symbol $\displaystyle{\frac{dy}{dx}}$ . It means the vertical distance between the current point $A(x_0, y_0)$ , where $y_0 = f(x_0)$ , and the point $C$ on the tangent line $y = mx + c$ , where $m$ is the slope of the tangent line. In other words,

$dy = m~dx$

$\displaystyle{dy = \left[ \left( \frac{d}{dx} \right) y \right] dx}$

The relationship of $\Delta y$ and $dy$ is that

$\displaystyle{\Delta y = \frac{dy}{dx} \Delta x + \text{higher order terms}}$

$\displaystyle{\Delta y = \frac{dy}{dx} dx + \text{higher order terms}}$

$\Delta y = dy + \text{higher order terms}$

Similarly, for functions of 2 variables:

$\displaystyle{\Delta f(x,y) = \frac{\partial f}{\partial x} \Delta x + \frac{\partial f}{\partial y} \Delta y + \text{higher order terms}}$

$\displaystyle{df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy}$

For functions of 3 variables:

$\displaystyle{df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy + \frac{\partial f}{\partial z} dz}$

$\displaystyle{\frac{df}{dt} = \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt} + \frac{\partial f}{\partial z}\frac{dz}{dt}}$

— Me@2018-07-15 09:30:29 PM

多項選擇題 6

Posted on May 22, 2018 by rpflee

Multiple Choices 6

這段改編自 2010 年 8 月 24 日的對話。

有時，一題物理 MC（多項選擇題）會，同時有數學做法和物理做法。

那時，你就先用物理方法做一次，再用數學方法做多一次，以作驗算。

（問：哪有那麼多的時間？）

之前講過，那些做法，必須透過考試前，平日多加收集和練習而來；並不是在考試中途，才花額外時間發明。

— Me@2018-05-22 06:02:40 PM

Van der Waals equation 1.2

Posted on May 16, 2018 by rpflee

Whether $X_{\text{measured}}$ is bigger or smaller than $X_{\text{ideal}}$ ultimately depends on the assumptions and definitions used in the derivation of the ideal gas equation itself.

In the ideal gas equation derivation, the volume used in the equation refers to the volume that the gas molecules can move within. So

$V_{\text{ideal}} = V_{\text{available for a real gas' molecules to move within}}$

Then, when deriving the pressure, it is assumed that there are no intermolecular forces among gas molecules. So

$P_{\text{ideal}} = P_{\text{assuming no intermolecular forces}}$

These are the reasons that

$V_{\text{ideal}} < V_{\text{measured}}$

$P_{\text{ideal}} > P_{\text{measured}}$

—

$P_{\text{ideal}} V_{\text{ideal}} = nRT$

$\left(P_\text{measured} + a\left(\frac{n}{V}\right)^2\right) \left(V_\text{measured}-nb\right) = nRT$

— Me@2018-05-16 07:12:51 PM

~~~

… the thing to keep in mind is that the “pressure we use in the ideal gas law” is not the pressure of the gas itself. The pressure of the gas itself is too low: to relate that pressure to “pressure for the ideal gas law” we have to add a number. While the volume occupied by the real gas is too large – the “ideal volume” is less than that. – Floris Sep 30 ’16 at 17:34

— Physics Stackexchange

Physics Town

continues

Category Archives: study

（反對）開夜車 4.2

（反對）開夜車 4.1

追憶逝水年華, 3

（反對）開夜車 2.5

（反對）開夜車 2.4

（反對）開夜車 2.3

（反對）開夜車 2.2

（反對）開夜車 2.1

Ken Chan 時光機 2.2

Ken Chan 時光機 2.1

迷宮直升機 5.3

迷宮直昇機 5.2

Ken Chan 時光機 1.4.1

Ken Chan 時光機 1.3

Ken Chan 時光機 1.2

Ken Chan 時光機 1.1

The Jacobian of the inverse of a transformation

Chain Rule of Differentiation

多項選擇題 6

Van der Waals equation 1.2