Ex 2.1-2 Particle in a Box

Posted on March 5, 2023 by rpflee

Quantum Methods with Mathematica

Reproduce Figure 2.1-1 …

~~~

phi[n_, x_] := Sin[n Pi x]

p[n_] := Plot[phi[n,x],{x,0,1}]

GraphicsColumn[{p[1], p[2], p[3]}]

— Me@2023-03-03 01:30:46 PM

Ex 2.1-1 Particle in a Box

Posted on December 17, 2022 by rpflee

Remove["Global`*"]

hbar := \[HBar]

H[V_] @ psi_  := -hbar^2/(2m) D[psi,{x,2}] + V psi

SchD[V_] @  psi_ := H[V] @ psi - En psi

SchD[V[x]] @ psi[x] == 0 // TeXForm

$\displaystyle{-\text{En} \psi (x)-\frac{\hbar ^2 \psi ''(x)}{2 m}+\psi (x) V(x)=0}$

phi[n_, x_] := Cn Sin[n Pi x/L]

SchD[0] @ phi[n,x] == 0 // ExpandAll

SchD[0] @ phi[n,x] / phi[n,x] == 0 // Simplify // TeXForm

$\displaystyle{2 \text{En} L=\frac{\pi ^2 n^2 \hbar ^2}{L m}}$

Starting with a linear superposition A E^(Ikx) + B E^(-Ikx) of independent plane waves, where A and B are constants, verify the box eigen-functions and eigen-energies given above.

Thus, show that this superposition is a solution of the Schrodinger equation and, by invoking the boundary condition, that k -> n Pi/L.

— Quantum Methods with Mathematica

phi[k_, x_] := A E^(I k x) + B E^(- I k x)

eq1 := SchD[0] @ phi[k,x]/phi[k,x] == 0 // Simplify

Ek[k_] := En /. Solve[eq1, En] [[1]]

Ek[k] // TeXForm

$\displaystyle{\frac{k^2 \hbar ^2}{2 m}}$

The boundary conditions are $\displaystyle{\phi_{x=0} = \phi_{x=L} = 0}$ .

$\displaystyle{ \begin{aligned} A+B&=0 \\ A e^{i k L}+B e^{-i k L}&=0 \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} e^{i k L} - e^{-i k L}&=0 \\ \end{aligned}}$

Solve[E^(I k L) - E^(-I k L) == 0, k] // Simplify

$\displaystyle{ \left\{k\to -\frac{2 \pi c_1}{L}\text{ if }c_1\in \mathbb{Z}, ~~~k\to -\frac{2 \pi c_1+\pi }{L}\text{ if }c_1\in \mathbb{Z} \right\}}$

$\displaystyle{ =\left\{k\to \frac{n \pi }{L}\text{ if }n \in \mathbb{Z}\right\}}$

phi[n_, x_] := Cn Sin[n Pi x/L]

norm[n_] = Cn /.
    Solve[
        Integrate[ phi[n,x]^2, {x,0,L}] == 1 /.
            Sin[m_Integer n Pi] -> 0, 
        Cn
    ] [[1]] // TeXForm

$\displaystyle{ -\frac{\sqrt{2}}{\sqrt{L}} }$

It’s interesting to note in passing that the 1D box eigenfunctions are also classically the eigenfunctions of a taut string. However, whereas the quantum mechanical energies scale as n^2, the classical eigenfrequencies of the string’s normal modes are linear in n. This is a consequence of the classical wave equation being second order in time in contrast to the quantum wave equation being first order.

— Quantum Methods with Mathematica

— Me@2022-12-16 10:23:45 AM

Ex 1.2-1 Stationary States

Posted on November 28, 2022 by rpflee

Quantum Methods with Mathematica

Assume a wavefunction of the form psi[x, t] == f[t] psi[x] and perform a separation of variables on the wave equation.

Show that f[t] = E^(-I w t) where h w is the separation constant. Try the built-in function DSolve.

Equate h w to the Energy by evaluating the [expected] value of hamiltonian[V] in the state psi[x, t].

~~~

Remove["Global`*"]


hbar := \[HBar]

H[V_] @ psi_  := -hbar^2/(2m) D[psi,{x,2}] + V psi



psi[x_,t_] := f[t] psi[x]

I hbar D [psi[x,t],t] == H[V] @ psi[x, t]

I hbar D [psi[x,t],t] / psi[x,t] == H[V] @ psi[x,t] / psi[x,t]

$\displaystyle{i \hbar \psi (x) f'(t)=V f(t) \psi (x)-\frac{\hbar ^2 f(t) \psi ''(x)}{2 m}}$

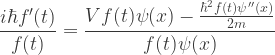
$\displaystyle{\frac{i \hbar f'(t)}{f(t)}=\frac{V f(t) \psi (x)-\frac{\hbar ^2 f(t) \psi ''(x)}{2 m}}{f(t) \psi (x)}}$

E1 := I hbar D [psi[x,t],t] / psi[x,t] == H[V] @ psi[x,t] / psi[x,t]

Simplify[E1]

$\displaystyle{\frac{1}{2} \hbar \left(\frac{\hbar \psi ''(x)}{m \psi (x)}+\frac{2 i f'(t)}{f(t)}\right)=V}$

E2 := - 1/2 hbar hbar (D[D[psi[x],x],x]/(m psi[x])) == hbar omega

DSolve[E2, psi[x], x]


E3 := 1/2 hbar 2 i D[f[t],t] / f[t] == hbar omega

DSolve[E3, f[t], t]

$\displaystyle{\left\{\left\{\psi (x)\to c_1 \cos \left(\frac{\sqrt{2} \sqrt{m} \sqrt{\omega } x}{\sqrt{\hbar }}\right)+c_2 \sin \left(\frac{\sqrt{2} \sqrt{m} \sqrt{\omega } x}{\sqrt{\hbar }}\right)\right\}\right\}}$

$\displaystyle{\left\{\left\{f(t)\to c_1 e^{\frac{\omega t}{i}}\right\}\right\}}$


k

psi[x_] := c E^(I k x)

psi[x]

f[t_] := E^(-I omega t)

f[t]

psi[x_,t_] := f[t] psi[x]

psi[x,t]

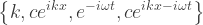
$\displaystyle{ \left\{k,c e^{i k x},e^{-i \omega t},c e^{i k x-i \omega t}\right\} }$

E4 := Conjugate[psi[x,t]] H[0] @ psi[x,t]

E4

E5 := Simplify[E4]

E5

k := Sqrt[2 m omega / hbar]

Refine[E5, {Element[{c, omega, m, t, hbar, k, x}, Reals]}]

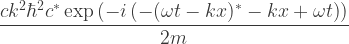
$\displaystyle{ \frac{c k^2 \hbar ^2 c^* \exp \left(-i \left(-(\omega t-k x)^*-k x+\omega t\right)\right)}{2 m} }$

$\displaystyle{ = c^2 \omega \hbar }$

E6 := Conjugate[psi[x,t]] psi[x,t]

Simplify[E6]

$\displaystyle{ c c^* \exp \left(-i \left(-(\omega t-k x)^*-k x+\omega t\right)\right) }$

$\displaystyle{ = c^2 }$

$\displaystyle{\begin{aligned} \langle E \rangle &= \frac{\int_{-\infty}^{\infty} \psi^* H_{V=0} \psi dx}{\int_{-\infty}^{\infty} \psi^* \psi dx} \\ \\ &= \frac{c^2 \omega \hbar \int_{-\infty}^{\infty} dx}{c^2 \int_{-\infty}^{\infty} dx} \\ \\ &= \omega \hbar \\ \end{aligned}}$

— Me@2022-11-26 07:17:29 PM

Euler problem 8.3

Posted on November 24, 2022 by rpflee

Directory[]

mString := Import["n.txt"]

nString := StringDelete[mString, "\n" | "\r"]

nList := Map[FromDigits, Characters[nString]]

take13[lst_] := Times @@ Take[lst,13]

Fmax13n[lst_, n_] := If[Length[lst] < 13,
                        n,
                        With[{t13 = take13[lst]},
                            If[n > t13,
                                Fmax13n[Rest[lst], n],
                                Fmax13n[Rest[lst], t13]]]]

Fmax13n[nList, 0]

Wmax13n[lst_, n_] := Which[
                        Length[lst] < 13, n,
                        t13 = take13[lst];
                            n > t13, Wmax13n[Rest[lst], n],
                            True, Wmax13n[Rest[lst], t13]]

Wmax13n[nList, 0]

Fmax13n[nList, 0] - Wmax13n[nList, 0]

— colorized by palette fm

— Me@2022-11-24 05:51:56 PM

Problem 14.5d1.2.2

Posted on November 23, 2022 by rpflee

A First Course in String Theory

The generating function is an infinite product:

$\displaystyle{ \begin{aligned} \alpha' M_L^2: \end{aligned}}$

$\displaystyle{\begin{aligned} &f_{L, NS+}(x) \\ &= a_{NS+} (r) x^r \\ &= \frac{1}{x} \prod_{r=1}^\infty \frac{(1 + x^{r-\frac{1}{2}})^{32}}{(1 - x^r)^8} \\ \end{aligned}}$

To evaluate the infinite product, you can use Mathematica (or its official free version Wolfram Engine) with the following commands:

TeXForm[
    HoldForm[
        (1/x)*Product[
                 (1+x^(r-1/2))^32/(1-x^r)^8,
                 {r, 1, Infinity}]]]

f[x_] := (1/x)*Product[
                 (1+x^(r-1/2))^32/(1-x^r)^8,
                 {r, 1, Infinity}]

Print[f[x]]

TeXForm[f[x]]

TeXForm[Series[f[x], {x,0,3}]]




                     1        32
    QPochhammer[-(-------), x]
                  Sqrt[x]
------------------------------------
        1    32                    8
(1 + -------)   x QPochhammer[x, x]
     Sqrt[x]

$\displaystyle{ \begin{aligned} &f_{L, NS+}(x) \\ \end{aligned}}$

$\displaystyle{ \approx \frac{1}{x}+\frac{32}{\sqrt{x}}+504+5248 \, \sqrt{x}+40996 \, x+258624 \, x^{\frac{3}{2}}+1384320 \, x^{2}+6512384 \, x^{\frac{5}{2}} + ...}$