Broken

Posted on August 22, 2021 by rpflee

A: Before meeting you, my life is chaotic.

M: It is because you missed, me. With me, you are completed.

— Me@2021-06-07 06:16:29 PM

— Me@2021-08-22 05:40:53 PM

上山尋寶, 2

Posted on August 16, 2021 by rpflee

重點副作用 6.2 | The non-side-effect-ness of side-effects, 6.2

這段改編自 2010 年 4 月 24 日的對話。

其實，我們可以考慮改變方案。雖然有些課題，可能幾個小時，就可以完成，但是，我們可以每個星期，也講不同的課題。

留意，雖然個別課題的成果，只會花幾小時，但是那是指，事先已有課題的情況下。那些有趣而深刻的課題，簡稱「勁題目」，並不會從天而降。那些勁題目本身，大部分情況下，只會在你開始研究，將會花「幾年加幾年」的苦功知識時，才會引發得到。

所以，我們先企圖進攻那些大題目，無論它們長遠是否，對你直接有用；因為，過程之中，自然會引發很多技術細節。而那些技術細節，很多是你直接可用。

例如，剛才因為跟你研究，大學力學課本《Structure and Interpretation of Classical Mechanics》（SICM），而提及到一個程式語言 Scheme programming language。而又因為研究該程式語言，而提及了一個，特別的文字編輯程式 Notepad++。雖然，大學力學和程式語言 Scheme 本身，對你而言，只是工餘興趣，但是，Notepad++ 卻是日常生活也有用。

原初辛苦上山的目的是，傳說中，山頂上的寶藏。但是，上到山頂後，才發現最珍貴的寶藏，反而是沿途找到的那些。

— Me@2021-08-16 04:31:19 PM

1986, 2

Posted on August 13, 2021 by rpflee

— Me@2021-08-13 04:52:08 PM

Ex 1.21 The dumbbell, 3.2

Posted on August 10, 2021 by rpflee

Structure and Interpretation of Classical Mechanics

c. Make a change of coordinates to a coordinate system with center of mass coordinates $\displaystyle{x_{cm}}$ , $\displaystyle{y_{cm}}$ , angle $\displaystyle{\theta}$ , distance between the particles $\displaystyle{c}$ , and tension force $\displaystyle{F}$ . Write the Lagrangian in these coordinates, and write the Lagrange equations.

~~~

[guess]

…

$\displaystyle{ \begin{aligned} m_0 \ddot y_0 &= F \sin \theta \\ m_0 \ddot x_0 &= F \cos \theta \\ m_1 \ddot y_1 &= -F \sin \theta \\ m_1 \ddot x_1 &= -F \cos \theta \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} y_{cm} &= \frac{m_0 y_0 + m_1 y_1}{m_0 + m_1} \\ x_{cm} &= \frac{m_0 x_0 + m_1 x_1}{m_0 + m_1} \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} \ddot y_{cm} &= \frac{F \sin \theta - F \sin \theta}{m_0 + m_1} = 0 \\ \ddot x_{cm} &= \frac{F \cos \theta - F \cos \theta}{m_0 + m_1} = 0 \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} y_0 &= y_{cm} - \frac{m_1}{M} c(t) \sin \theta \\ x_0 &= x_{cm} - \frac{m_1}{M} c(t) \cos \theta \\ y_1 &= y_{cm} + \frac{m_0}{M} c(t) \sin \theta \\ x_1 &= x_{cm} + \frac{m_0}{M} c(t) \cos \theta \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} x_1 - x_0 &= \frac{m_0}{M} c(t) \cos \theta + \frac{m_1}{M} c(t) \cos \theta \\ &= c(t) \cos \theta \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} \dot x_1 - \dot x_0 &= \dot c(t) \cos \theta - c(t) \dot \theta \sin \theta \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} \ddot x_1 - \ddot x_0 &= \ddot c(t) \cos \theta - \dot c(t) \dot \theta \sin \theta - \dot c(t) \dot \theta \sin \theta - c(t) \ddot \theta \sin \theta - c(t) \dot \theta^2 \cos \theta\\ \end{aligned}}$

$\displaystyle{ \begin{aligned} y_1 - y_0 &= c(t) \sin \theta \\ \dot y_1 - \dot y_0 &= \dot c(t) \sin \theta + c(t) \dot \theta \cos \theta \\ \ddot y_1 - \ddot y_0 &= \ddot c(t) \sin \theta + \dot c(t) \dot \theta \cos \theta + \dot c(t) \dot \theta \cos \theta + c(t) \ddot \theta \cos \theta - c(t) \dot \theta^2 \sin \theta \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} m_0 \ddot y_0 &= F \sin \theta \\ m_0 \ddot x_0 &= F \cos \theta \\ m_1 \ddot y_1 &= -F \sin \theta \\ m_1 \ddot x_1 &= -F \cos \theta \\ \end{aligned}}$

When $\displaystyle{\dot c(t) = 0}$ and $\displaystyle{\ddot c(t) = 0}$ ,

$\displaystyle{ \begin{aligned} \ddot x_1 - \ddot x_0 &= - c(t) \ddot \theta \sin \theta - c(t) \dot \theta^2 \cos \theta \\ - \left( \frac{1}{m_1} + \frac{1}{m_1} \right) F \cos \theta &= - c(t) \ddot \theta \sin \theta - c(t) \dot \theta^2 \cos \theta\\ \end{aligned}}$

$\displaystyle{ \begin{aligned} \ddot y_1 - \ddot y_0 &= ... \\ - \left( \frac{1}{m_1} + \frac{1}{m_0} \right) F \sin \theta &= c(t) \ddot \theta \cos \theta - c(t) \dot \theta^2 \sin \theta \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} \tan \theta &= \frac{ c(t) \ddot \theta \cos \theta - c(t) \dot \theta^2 \sin \theta }{- c(t) \ddot \theta \sin \theta - c(t) \dot \theta^2 \cos \theta} \\ &= \frac{ \ddot \theta - \dot \theta^2 \tan \theta }{- \ddot \theta \tan \theta - \dot \theta^2} \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} \tan \theta \left( - \ddot \theta \tan \theta - \dot \theta^2 \right) &= \ddot \theta - \dot \theta^2 \tan \theta \\ &... \\ 0 &= \ddot \theta (1 + \tan^2 \theta) \\ \ddot \theta &= 0 \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} - \left( \frac{1}{m_1} + \frac{1}{m_0} \right) F \sin \theta &= c(t) \ddot \theta \cos \theta - c(t) \dot \theta^2 \sin \theta \\ - \left( \frac{1}{m_1} + \frac{1}{m_1} \right) F \cos \theta &= - c(t) \ddot \theta \sin \theta - c(t) \dot \theta^2 \cos \theta\\ \end{aligned}}$

Let $\displaystyle{\frac{1}{\mu} = \left( \frac{1}{m_1} + \frac{1}{m_1} \right)}$ and since $\displaystyle{\ddot \theta = 0}$ ,

$\displaystyle{ \begin{aligned} - \frac{1}{\mu} F \sin \theta &= - c(t) \dot \theta^2 \sin \theta \\ - \frac{1}{\mu} F \cos \theta &= - c(t) \dot \theta^2 \cos \theta\\ \end{aligned}}$

Since $\displaystyle{\sin \theta}$ and $\displaystyle{\cos \theta}$ cannot be both zero at the same time,

$\displaystyle{ \begin{aligned} - \frac{1}{\mu} F &= - c(t) \dot \theta^2 \\ \end{aligned}}$

Put $\displaystyle{c(t) = l}$ ,

$\displaystyle{ \begin{aligned} \frac{1}{\mu} F &= l \dot \theta^2 \\ \dot \theta^2 &= \frac{1}{l \mu} F \\ \end{aligned}}$

[guess]

— Me@2021-08-08 05:41:21 PM

Logical arrow of time, 9.4

Posted on August 7, 2021 by rpflee

The second law of thermodynamics’ derivation (Ludwig Boltzmann’s H-theorem) is with respect to an observer.

How does an observer keep losing microscopic information about a system?

— Me@2017-02-12 07:37:54 PM

This drew the objection from Loschmidt that it should not be possible to deduce an irreversible process from time-symmetric dynamics and a time-symmetric formalism: something must be wrong (Loschmidt’s paradox).

The resolution (1895) of this paradox is that the velocities of two particles after a collision are no longer truly uncorrelated. By asserting that it was acceptable to ignore these correlations in the population at times after the initial time, Boltzmann had introduced an element of time asymmetry through the formalism of his calculation.

— Wikipedia on Molecular chaos

Physical entropy’s value is with respect to an observer.

— Me@2017-02-12 07:37:54 PM

This “paradox” can be explained by carefully considering the definition of entropy. In particular, as concisely explained by Edwin Thompson Jaynes, definitions of entropy are arbitrary.

As a central example in Jaynes’ paper points out, one can develop a theory that treats two gases as similar even if those gases may in reality be distinguished through sufficiently detailed measurement. As long as we do not perform these detailed measurements, the theory will have no internal inconsistencies. (In other words, it does not matter that we call gases A and B by the same name if we have not yet discovered that they are distinct.) If our theory calls gases A and B the same, then entropy does not change when we mix them. If our theory calls gases A and B different, then entropy does increase when they are mixed. This insight suggests that the ideas of “thermodynamic state” and of “entropy” are somewhat subjective.

— Wikipedia on The mixing paradox

— Wikipedia on Gibbs paradox

Graduate school

Posted on August 6, 2021 by rpflee

Turn my life into an ideal graduate school. Be my own professor.

— Me@2011.05.26

Doing real research, doing real teaching.

— Me@2021-08-06 05:03:16 PM

To realize is to realize, 1.3

Posted on July 27, 2021 by rpflee

搜神記 2

The ultimate self-fulfilling prophecies:

1. free will or not

2. god or no god

3. afterlife or not

4. future spouse exists or not

Why self-fulfilling?

2. god or no god

Whether “god” exists or not depends on your definition of the word “god”.

In some definitions, god does not exist, because of the definitions’ self-contradictory nature. For example, god is good but he wants you to suffer for no reason.

In some definitions, god is possible to exist. For example, a god is any being that has a higher level of consciousness than a human being.

We can say that a human being’s consciousness is higher than a dog’s, in the sense that a human can understand things that a dog cannot. For example, most dogs do not understand what a computer is.

Similarly, a dog’s consciousness is higher than an ant’s. An ant’s consciousness is higher than a tree’s. A tree’s consciousness is higher than a rock’s.

In the opposite direction, it is highly possible that in this universe, there are beings that have a higher level of consciousness than human beings. It is highly unlikely that human beings are the highest beings.

Even within the human being species itself, different people can have different levels of consciousness. Even within a single person’s lifetime, one can be at different levels at different ages.

In some definitions, god can exist. You become that god.

In those cases, whether god exists or not depends on whether YOU are willing to become that god, taking up his responsibilities.

— Me@2021-07-26 05:49:53 PM

1995, 2

Posted on June 9, 2021 by rpflee

— 1995

物理一個字：力學第一步

Posted on June 7, 2021 by rpflee

This is my first created video.

Please click, like, share, and subscribe!

— Me@2021-06-07 05:00:34 PM

For all, 8.2

Posted on May 31, 2021 by rpflee

“For all” without range creates infinity, which creates paradoxes.

— Me@2017-02-20 06:09:07 PM

What is magic

Posted on May 30, 2021 by rpflee

Science is the real magic.

What you know is science; what you do not know is magic.

Life is a process of turning magic into science.

— Me@2016-11-20 09:14:06 AM

一萬個小時 3.4

Posted on May 25, 2021 by rpflee

重點副作用 6 | The non-side-effect-ness of side-effects, 6

這段改編自 2010 年 4 月 24 日的對話。

現在，有三個概念混淆在一起。我們先釐清一下。

1. 幾乎

任何學問，或者才藝，如果要訓練自己，純熟到足以用來維生賺錢，或者娛樂滿足，需要的時間幅度是，一日幾小時，持續一兩年，才會開竅；然後，再持續一兩年，才會知道自己，在該門學問才藝，為何會開竅，開了什麼竅；又再過一兩年，才會有能力教人，如何在該門學問才藝開竅。

2. 過程中的一個重要環節是，會領悟到一些洞見。

3. 雖然要「自己領悟」第二點中的洞見，來自第一點中的「幾年加幾年」過程，但是，如果只是「吸收別人已知的」知識本身，絶不需要花「幾年加幾年」。有時，甚至只是，花數個小時就可以。

「學習」的意思正正就是，自己毋須親身經歷（例如）四年，也可以獲取本來要四年，才發掘得到的成果。

4. (1.) 但是，「知道」本身，並不代表自己有足夠功力去「運用」，而「運用」則是，第一點的水平。不過，如果中途有第三點，即是別人情報資料上的提點，你就可以走少很多冤往路。那樣，原本是（例如）十年的過程，可以壓縮到（例如）三年。

剛才你提到：「

你的講法是，有些知識，你只需要幾個小時，就可以傳授給我，不成課程，因為時間所需太短；而另一些知識，我就需要花「幾年加幾年」，才可以領會得到，不成課程，因為時間所需太長。

」

其實，我們可以考慮改變方案。雖然有些課題，可能幾個小時，就可以完成，但是，我們可以每個星期，也講不同的課題。

— Me@2021-05-23 04:39:54 PM

World Cup 98

Posted on May 21, 2021 by rpflee

— Me@2021-05-20 11:07:10 PM

2.10 A spacetime orbifold in two dimensions, 2

Posted on May 17, 2021 by rpflee

A First Course in String Theory

(a) Use the result of Problem 2.2, part (a), to recast (1) as

$\displaystyle{(x^+, x^-) \sim \left( e^{-\lambda} x^+, e^{\lambda} x^- \right)}$ , where $\displaystyle{e^\lambda \equiv \sqrt{\frac{1+\beta}{1-\beta}}}$ .

What is the range of $\lambda$ ? What is the orbifold fixed point? Assume now that $\beta > 0$ , and thus $\lambda > 0$ .

~~~

Range of $\displaystyle{\lambda}$ :

$\displaystyle{ \begin{aligned} 0 &< \beta < \infty \\ 1 &< \frac{1 + \beta}{1 - \beta} < \infty \\ 0 &< \ln \frac{1 + \beta}{1 - \beta} < \infty \\ 0 &< \frac{1}{2} \ln \frac{1 + \beta}{1 - \beta} < \infty \\ 0 &< \lambda < \infty \\ \end{aligned}}$

Fixed points:

$\displaystyle{ \begin{aligned} \begin{bmatrix} (x^+)' \\ (x^-)' \end{bmatrix} &= \begin{bmatrix} e^{- \lambda} x^+ \\ e^{\lambda} x^- \\ \end{bmatrix} \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} (x^+, x^-) &= (0, 0) \\ \end{aligned}}$

— Me@2021-05-16 06:31:12 PM

Logical arrow of time, 9.3

Posted on May 16, 2021 by rpflee

We label the time direction that we can remember as “past”.

If we could remember both time directions, we would remember infinite things, unless the future has an anti-big-bang.

Also “remembering the future” creates a meta-dox (aka paradox).

— Me@2013-08-11 8:25 AM

Genius 4

Posted on May 15, 2021 by rpflee

High school teachers are by nature non-intellectuals; students are by nature intellectuals.

— Me@2011.08.23

As a mathematician there is a story I hear a lot. It tends to come up whenever I tell someone what I do for the first time, and they admit that they don’t really like, or aren’t very good at, mathematics. In almost every case, if I bother to ask (and these days I usually do), I find that the person, once upon a time, was good at and liked mathematics, but somewhere along the way they had a bad teacher, or struck a subject they couldn’t grasp at first, and fell a bit behind. From that point on their experiences of mathematics is a tale of woe: because mathematics piles layer upon layer, if you fall behind then you find yourself in a never ending game of catch-up, chasing a horizon that you never seem to reach; that can be very dispiriting and depressing.

— Zen and the Art of Mathematics

— The Narrow Road

All children are born geniuses; 9999 out of every 10000 are swiftly, inadvertently degeniusized by grownups.

— Buckminster Fuller

千里共嬋娟

Posted on May 15, 2021 by rpflee

尋覓 2.2.3.5 | Passion Test 2.3 | 二百萬 4

如果你覺得你女朋友，會阻礙你工作進度，或者是你時間負擔的話，你倆大概由始至終，就不應在一起；你倆根本不是，對方的另一半。

第三，太陽會發光，月亮不會。但是，月亮單單是存在本身，就已經透過反射，為地球黑夜一面，帶來不止的光芒。

發現「質量守恆定律」的，是一位化學家，名叫拉瓦節（Antoine-Laurent de Lavoisier）。他的正識是一位稅務官。因為高薪厚職，他有充足的金錢，去購買很多高級精準的化學儀器，以作化學研究之用。他的其中一個科學功績是，透過他的一些實驗，印證了「質量守恆定律」。

拉瓦節的太太 Marie-Anne Pierette Paulze，同時是他的助手 —— 為拉瓦節把文章翻譯成外語，從而把拉瓦節的化學研究成果，發揚光大。

拉瓦節太太的化學造詣，不及丈夫；而拉瓦節的文字功力，亦不及太太。但是，他們卻是夢幻組合，合力發表了，很多改變歷史的作品。

化學方面，拉瓦節是太陽，太太是月亮；文字方面，太太是太陽，拉瓦節是月亮。

那是直接的合作。但是，有時，另一半單單是存在本身，就令你可以創作到，一些原本不可能存在的作品，又名「神作」。

例如，作家如果沒有（現在或未來的）知己知音，其實不會有心神動機（心機），去開始創作。即使有因為金錢的引誘，而夾硬創作，結果也不會是神作，只會是鬼作，連自己也不想閱讀。

相反，作家如果有（現在或未來的）知己知音的話，創作的過程就如，穿梭時空，探索宇宙；創作的結果就成，神來之筆，扣人心弦。

— Me@2021-05-14 11:02:51 PM

1990s, 9

Posted on May 11, 2021 by rpflee

— Me@2021-05-11 10:04:18 PM

Ex 1.21 The dumbbell, 2.2.2

Posted on May 11, 2021 by rpflee

[guess]


(define (KE-particle m v)
  (* 1/2 m (square v)))

(define ((L-free-constrained m0 m1 l) local)
  (let* ((extract (extract-particle 2))
	 (p0 (extract local 0))
	 (q0 (coordinate p0))
	 (qdot0 (velocity p0))
 
	 (p1 (extract local 1))
	 (q1 (coordinate p1))
	 (qdot1 (velocity p1))
 
	 (F (ref (coordinate local) 4)))

    (- (+ (KE-particle m0 qdot0)
	      (KE-particle m1 qdot1))
          (U-constraint q0 q1 F l))))

(let ((L (L-free-constrained 'm_0 'm_1 'l)))
  (show-expression
   ((compose L (Gamma q-rect)) 't)))

$\displaystyle{ \frac{1}{2} m_0 \left( \dot x_0^2 + \dot y_0^2 \right) + \frac{1}{2} m_1 \left( \dot x_1^2 + \dot y_1^2 \right) + \frac{F}{2 l} \left( l^2 - y_1^2 + 2 y_0 y_1 - x_1^2 + 2 x_0 x_1 - y_0^2 - x_0^2 \right) }$

$\displaystyle{ = \frac{1}{2} m_0 \left( \dot x_0^2 + \dot y_0^2 \right) + \frac{1}{2} m_1 \left( \dot x_1^2 + \dot y_1^2 \right) - \frac{F}{2 l} \left[ (y_1 - y_0)^2 + (x_1 - x_0)^2 - l^2 \right] }$


(define ((local_ m0 m1 l) local)
  (let* ((extract (extract-particle 2))
	 (p0 (extract local 0))
	 (q0 (coordinate p0))
	 (qdot0 (velocity p0))
 
	 (p1 (extract local 1))
	 (q1 (coordinate p1))
	 (qdot1 (velocity p1))
 
	 (F (ref (coordinate local) 4)))
    local))

(show-expression
 ((compose (local_ 'm_0 'm_1 'l) (Gamma q-rect)) 't))


(define ((p0_ m0 m1 l) local)
  (let* ((extract (extract-particle 2))
	 (p0 (extract local 0))
	 (q0 (coordinate p0))
	 (qdot0 (velocity p0))
 
	 (p1 (extract local 1))
	 (q1 (coordinate p1))
	 (qdot1 (velocity p1))
 
	 (F (ref (coordinate local) 4)))
    p0))
 
(show-expression
 ((compose (p0_ 'm_0 'm_1 'l) (Gamma q-rect)) 't))


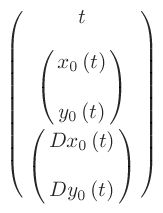
(define ((p1_ m0 m1 l) local)
  (let* ((extract (extract-particle 2))
	 (p0 (extract local 0))
	 (q0 (coordinate p0))
	 (qdot0 (velocity p0))
 
	 (p1 (extract local 1))
	 (q1 (coordinate p1))
	 (qdot1 (velocity p1))
 
	 (F (ref (coordinate local) 4)))
    p1))
 
(show-expression
 ((compose (p1_ 'm_0 'm_1 'l) (Gamma q-rect)) 't))

[guess]

— based on /sicmutils/sicm-exercises

— Me@2021-04-27 05:03:59 PM

Goodstein’s theorem

Posted on May 9, 2021 by rpflee

[guess]

Goodstein’s theorem is an example that sometimes a finite result requires the existence of infinity in its proof.

— Me@2021-05-09 11:06:34 PM

Goodstein’s theorem itself assumes that there is an infinite number of natural numbers, so it is not really a finite result.

— Me@2017-02-20 06:16:28 PM

[guess]

Physics Town

continues

Broken

上山尋寶, 2

1986, 2

Ex 1.21 The dumbbell, 3.2

Logical arrow of time, 9.4

Graduate school

To realize is to realize, 1.3

1995, 2

物理一個字：力學第一步

For all, 8.2

What is magic

一萬個小時 3.4

World Cup 98

2.10 A spacetime orbifold in two dimensions, 2

Logical arrow of time, 9.3

Genius 4

千里共嬋娟

1990s, 9

Ex 1.21 The dumbbell, 2.2.2

Goodstein’s theorem