30112002
1. A secret is not a secret if it is known by more than one person.
.
.
2022.11.21 Monday ACHK

30112002
1. A secret is not a secret if it is known by more than one person.
.
.
2022.11.21 Monday ACHK
數學教育 1.2 | Personality | Break free | People don’t change | Choose around | Change the world, 2
這段改編自 2010 年 4 月 24 日的對話。
.
每人都有對自己的最先責任,和最終責任。其他人對你,則沒有必然責任。你對其他人,亦沒有。
.
那是一個好重要的常識。那是 Stephen Covey 在他那本《First Things First》中教的。
記住,一個人(甲)並不能夠改變,另一個人(乙);除非,乙自己想改變。
當乙自己想改變時,不知道如何執行,你可以教他方法;或者執行時過份緩慢,你可以教他加速。
但是,如果乙本身沒有意願,去改變自己的話,那就一切已失去,不可以再追。
.
老師的責任,是把學生的學習動機,乘大一千倍。
只要有學習動機,無論是多麼小,乘大一千倍後,都可以威力驚人。
但是,如果學習動機是零的話,零乘一千還是零。
— Me@2010.01.29
— Me@2022-11-20 07:46:26 PM
.
.
2022.11.21 Monday (c) All rights reserved by ACHK
Euler problem 8.2
.

.
import Data.Char max13 lst = max13n lst 0 where max13n lst n | (length lst) < 13 = n | n > take13 = max13n (tail lst) n | otherwise = max13n (tail lst) take13 where take13 = product (take 13 lst) str <- readFile "n.txt" max13 (map (fromIntegral . digitToInt) . concat . lines $ str)
.
— Me@2022-11-19 12:04:41 PM
.
.
2022.11.19 Saturday (c) All rights reserved by ACHK
Functional Differential Geometry
.
~~~
(define R2 (make-manifold R^n 2)) (define U (patch 'origin R2)) (define R2-rect (coordinate-system 'rectangular U)) (define R2-polar (coordinate-system 'polar/cylindrical U)) (define R2-rect-chi (chart R2-rect)) (define R2-rect-chi-inverse (point R2-rect)) (define R2-polar-chi (chart R2-polar)) (define R2-polar-chi-inverse (point R2-polar)) (show-expression ((compose R2-polar-chi R2-rect-chi-inverse) (up 'x_0 'y_0)))
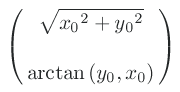
(show-expression ((D (compose R2-rect-chi R2-polar-chi-inverse)) (up 'r_0 'theta_0)))
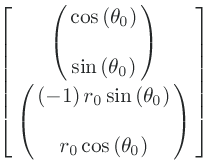
(define R2->R (-> (UP Real Real) Real)) (define f (compose (literal-function 'f-rect R2->R) R2-rect-chi)) (define R2-rect-point (R2-rect-chi-inverse (up 'x_0 'y_0))) (define corresponding-polar-point (R2-polar-chi-inverse (up (sqrt (+ (square 'x_0) (square 'y_0))) (atan 'y_0 'x_0)))) (f R2-rect-point) (f corresponding-polar-point) (show-expression (f R2-rect-point)) (show-expression (f corresponding-polar-point))

— Me@2022-11-18 11:22:36 AM
.
.
2022.11.18 Friday (c) All rights reserved by ACHK
time ~ change
time travel ~ undo the change
— Me@2016-07-20 06:16:34 AM
.
.
2022.11.16 Wednesday (c) All rights reserved by ACHK
權力來源 3
.
political power
~ market power
~ the power due to being the default
~ network effect
— Me@2022-11-09 04:02:00 PM
.
.
2022.11.15 Tuesday (c) All rights reserved by ACHK
排列組合 1.6 | nCr, 0.6
.
.
.
2022.11.14 Monday (c) All rights reserved by ACHK
Euler problem 8.1
.
.
73167176531330624919225119674426574742355349194934
96983520312774506326239578318016984801869478851843
85861560789112949495459501737958331952853208805511
12540698747158523863050715693290963295227443043557
66896648950445244523161731856403098711121722383113
62229893423380308135336276614282806444486645238749
30358907296290491560440772390713810515859307960866
70172427121883998797908792274921901699720888093776
65727333001053367881220235421809751254540594752243
52584907711670556013604839586446706324415722155397
53697817977846174064955149290862569321978468622482
83972241375657056057490261407972968652414535100474
82166370484403199890008895243450658541227588666881
16427171479924442928230863465674813919123162824586
17866458359124566529476545682848912883142607690042
24219022671055626321111109370544217506941658960408
07198403850962455444362981230987879927244284909188
84580156166097919133875499200524063689912560717606
05886116467109405077541002256983155200055935729725
71636269561882670428252483600823257530420752963450Find the thirteen adjacent digits in the 1000-digit number that have the greatest product. What is the value of this product?
(defun file-get-contents (filename) (with-open-file (stream filename) (let ((contents (make-string (file-length stream)))) (read-sequence contents stream) contents))) (defun file-get-lines (filename) (with-open-file (stream filename) (loop :for line = (read-line stream nil) :while line :collect line))) (file-get-lines #P"n.txt") (defun string-to-list (the-string) (loop :for char :across the-string :collect char)) (defun char-to-integer-list (char-list) (mapcar #'digit-char-p char-list)) (let ((the-digits (char-to-integer-list (string-to-list (remove #\newline (file-get-contents #P"n.txt")))))) (loop :for i :from 0 :to (- (length the-digits) 13) :maximize (apply #'* (subseq the-digits i (+ i 13)))))
.
— colorized by palette fm
— Me@2022-11-12 04:50:19 PM
.
.
2022.11.12 Saturday (c) All rights reserved by ACHK
A First Course in String Theory
.
(b) Repeat the analysis of three-dimensional electromagnetism starting with the Lorentz covariant formulation. Take , examine
, the Maxwell equations (3.34), and the relativistic form of the force law derived in Problem 3.1.
~~~
.
Eq. (3.20):
.
Eq. (3.33):
.
Eq. (3.34):
.
.
.
.
.
.
P. (3.1):
.
.
.
.
.
— Me@2022-11-08 03:46:01 PM
.
.
2022.11.10 Thursday (c) All rights reserved by ACHK
A singularity doesn’t have mass. Mass is a property of an object that exists in time. A (spacelike, e.g. Schwarzschild) singularity is not an object that exists in time. A singularity is a moment in time when time ends along with mass. Furthermore, a black hole does not have a center. The geometry of the Schwarzschild spacetime inside the horizon is an infinitely long 3-cylinder with a quickly shrinking circumference. Also, no black hole solution is valid inside the horizon, because all solutions assume a static metric, but it is not static inside the horizon.
— safesphere
— May 20, 2019 at 10:38
.
And if you wanted to say that the whole mass is obtained from the singularity, you won’t be able to get a good calculation because the integral over the singularity would be singular. Moreover, the space and time are really interchanged inside the black hole (the signs of the components
and
get inverted for
) so the exercise is in no way equivalent to a simple 3D volume integral of
. The Schwarzschild singularity, to pick the "simplest" black hole, is a moment in time, not a place in space. It is the final moment of life for the infalling observers. In a locally (conformally) Minkowski patch near the singularity with some causally Minkowskian coordinates
and
, the Schwarzschild singularity looks like a
hypersurface, not as
.
— Black hole mass can't be visualized as a property of the black hole interior
— Lubos Motl
.
.
2022.11.08 Tuesday ACHK
technical/skills
~ a collection of exceptions
~ something you cannot totally derive
— Me@2016-03-16 04:54:02 PM
.
.
2022.11.07 Monday (c) All rights reserved by ACHK
這段改編自 2021 年 12 月 15 日的對話。
.
Don’t spend your time making other people happy. Other people being happy is their problem. It’s not your problem. If you are happy, it makes other people happy.
— @naval
.
你在人生中,有一大部分問題,都是來自於,你以為你有責任,去解決其他人的問題。
在那愚善的年代,我不明白這一句。直到近年,我才深切體會到,它的意思。另一個版本是:
每人都有對自己的最先責任,和最終責任。其他人對你,則沒有必然責任。你對其他人,亦沒有。
.
當你覺得你一定、必須、任何時候,也有責任要,幫助任何他人時,那就是你摧毁自己(和他人)的人生之始。合理的版本是,
你先獨善其身;然後,行有餘力的話,就在有些時候,幫助有些應該幫助的人,如果當事人同意的話。
.
記住,起點是,你有責任,去解決你自己的問題,但是,你並沒有責任,去解決其他人的問題。有時,間中幫助人,並不是因為責任,而是基於愛心或情義。而「有時候,在你沒有責任幫時,仍然選擇幫」,正正是人性光輝之處。
精確一點用字的話:必須做的工作,為之「責任」;可做可不做的,為之「愛心」或「情義」。
.
既然可幫可不幫,那樣,什麼時候應該幫呢?
— Me@2022-11-05 12:54:58 PM
.
.
2022.11.06 Sunday (c) All rights reserved by ACHK
Structure and Interpretation of Classical Mechanics
.
An analogous result holds when the ‘s depend explicitly on time.
…
b. Show that, by adding a total time derivative, the Lagrangian can be written in the form , where
is a homogeneous quadratic form in the generalized velocities and
is independent of velocity.
~~~
The addition of a total time derivative to a Lagrangian does not affect whether the action is critical for a given path.
…
Moreover, the additional terms introduced into the action by the total time derivative appear only in the endpoint condition and thus do not affect the Lagrange equations derived from the variation of the action, …
— 1.6.4 The Lagrangian Is Not Unique
.
.
.
.
,
where
.
Since is a total time derivative,
.
Then, by choosing a suitable function , we can access a simple case that
.
.
.
.
This answer is not totally correct, since the generalized velocity, , should be a vector.
— Me@2022-11-01 08:58:52 AM
.
.
2022.11.02 Wednesday (c) All rights reserved by ACHK
One of Intel’s top executives once told me that he finally understood how things had changed in microprocessor business when someone asked him if he would accept delivery on an expensive new automobile if it was in perfect condition except for a big scratch on the door. After all, the car would deliver the same fuel economy, same performance, same cargo capacity, same expected service lifetime. But no, he paid for a perfect product, and that’s what he expected.
— IEEE Computer
— 2002.07.08
.
.
2022.10.31 Monday ACHK
75% -> vhdl
10% -> ps
15% -> transmission
~~~
EPROM: E = 0
G = 0
P = 1
~~~
Maths mid-term:
11/10/2011
.
.
2022.10.31 Monday (c) All rights reserved by ACHK
nCr, 0.5
.
.
.
2022.10.30 Sunday (c) All rights reserved by ACHK

— by this meme’s creator
.
(defun range (max &key (min 0) (step 1)) (loop :for n :from min :below max :by step collect n)) (defun sum-1-n (n) (/ (* n (+ n 1)) 2)) (defun sum (lst) (reduce #'+ lst)) (defun square (x) (* x x)) (- (square (sum-1-n 100)) (sum (mapcar #'square (range 101 :min 1)))) ; 25164150
.
— Me@2022-10-29 06:39:07 AM
.
.
2022.10.29 Saturday (c) All rights reserved by ACHK
Functional Differential Geometry
.
The metric for a unit sphere, expressed in colatitude and longitude
, is
Compute the Lagrange equations for motion of a free particle on the sphere …
~~~
(define ((L2 mass metric) place velocity) (* 1/2 mass ((metric velocity velocity) place))) (define ((Lc mass metric coordsys) state) (let ((x (coordinates state)) (v (velocities state)) (e (coordinate-system->vector-basis coordsys))) ((L2 mass metric) ((point coordsys) x) (* e v)))) (define the-metric (literal-metric 'g R2-rect)) (define L (Lc 'm the-metric R2-rect)) (L (up 't (up 'x 'y) (up 'vx 'vy))) (show-expression (L (up 't (up 'x 'y) (up 'v_x 'v_y))))

.
(show-expression (L (up 't (up 'theta 'phi) (up 'thetadot 'phidot))))
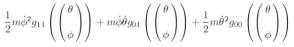
.
When and
,
.
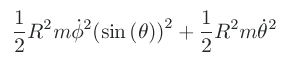
.
— Me@2022-10-27 10:30:50 AM
.
.
2022.10.28 Friday (c) All rights reserved by ACHK
superkuh 17 hours ago [–]
Coherence isn’t what you think it is. It is not an “alignment in phase” of the sinusoid, like all the lay diagrams show. It isn’t even being the same frequency. In the early days of quantum physics the light sources were mercury arc lamps (muliple freqs) that achieved coherence by shining through tiny pinholes.
https://web.archive.org/web/20220820182938/http://amasci.com/miscon/coherenc.html
Coherence is being a point source. Stars, except for our sun since it is too close, are coherent light sources.
— Hacker News
.
.
2022.10.27 Thursday ACHK
You must be logged in to post a comment.