…
Experiment C:
What if during Experiment A, the observer changes his mind to turn on the detector before the particle’s arrival?
Explanation X:
We should regard this whole process as an experiment-setup.
The probability patterns encoded in the quantum state is of this experiment-setup, which in this case is equivalent to Experiment B. With respect to this experiment-process/experiment-setup, the variable-to-be-measured is always in a mixed state.
The word “always” here means that a quantum state is not a physical state of a particle in physical spacetime during the experiment. Instead, it is a property (of a physical variable) of the experiment-setup (physical system) itself.
“Physical system” means the experimental-setup design, which includes not just objects and devices, but also operations.
.
However, for an experiment like Experiment C, doesn't the violation of Bell's inequality have proved that the spin of the particle is still in a superposition before the activation of the detector?
Let’s translate this question to a double-slit experiment version. (The consistency of the left detector and the right detector is as strange as the EPR consistency.)
Experiment C:
What if in the double-slit experiment, the detector is off when the particle is emitted, but the observer changes his mind to turn on the detector before the particle’s passing through of the double-slit plate?
Is the particle in a superposition or not when the detector is still off?
Instead of a superposition pure state, we should regard the particle path state as a mixed state, even before the detector is activated.
The reason is given in Explanation X.
.
However, for an experiment like Experiment C, doesn't the violation of Bell's inequality have proved that the path of the particle is still in a superposition before the activation of the detector?
The violation of Bell’s inequality should be interpreted in this way:
Experiment A:
If there is no detector activated throughout the experiment until the particle reaches the final screen, the resulting statistical pattern (aka the interference pattern) is possible only if the particle has no definite path. “An unknown but definite path exists” would not be able to create such statistics.
.
Experiment B:
If there is a detector activated since the beginning of the experiment, the particle path is in a mixed state since that beginning, meaning that the path is definite although unknown before measurement.
.
Experiment C:
What if in the double-slit experiment, the detector is off when the particle is emitted, but the observer changes his mind to turn on the detector before the particle’s passing through of the double-slit plate?
Is the particle in a superposition or not when the detector is still off?
After the detector is activated, the path is in a mixed state.
Before the detector is activated, regarding the path state as in a superposition or as in a mixed state makes no physical difference, because by definition, there is no measurement before the detector is activated.
Also, a superposition’s coefficients are always about the potential-activation of detectors.
A superposition state has a corresponding mixed state. The superposition coefficients can be modulus-squared to give the mixed state coefficients. That is the exact original meaning of the superposition coefficients. (This is the statistical interpretation given by Born rule.)
In other words, each coefficient in a superposition state by default encodes the probability of each potential measurement result.
.
However, in Experiment C, regarding the state as a superposition state before the activation of detector creates conceptual paradoxes, such as:
If the particle path variable has no definite state before measurement, how come the left detector and right detector always give consistent results?
This is the double-slit experiment version of the EPR paradox.
.
When the experimenter follows the plan of Experiment A, the particle path variable is always in a superposition, since the beginning of the experiment.
However, when he changes his mind to turn on the detector before the particle’s passing through of the double-slit plate, the particle path variable is always in a mixed state, since the beginning of the experiment.
Wouldn’t that create retro-causality?
It seems to be retro-causality, but it is not, because this description is a language shortcut only. The apparent violation of causality does not exist in the language longcut version, which is provided in Explanation X.
Also, due to the indistinguishability of identical particles, particle identities and thus particle trajectories are post hoc stories only.
.
In short, the violation of Bell’s inequality means that:
If there is no path detector activated throughout the experiment until the particle reaches the final screen, the path variable never has a definite value, known or unknown, throughout that experiment.
The violation of Bell’s inequality should not be applied to Experiment C, because it is not the case of “having no detector throughout the experiment”.
Also, note that we do not need the violation of Bell’s inequality to prove that the path variable has no definite state, known or unknown.
Just the interference pattern’s existence is already enough for us to do so.
— Me@2022-03-08 11:56:00 PM
.
.
2022.03.24 Thursday (c) All rights reserved by ACHK










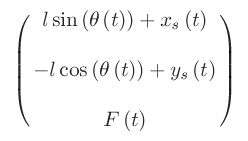


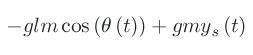

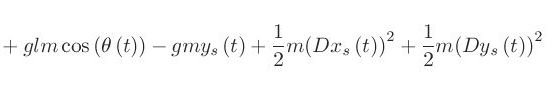

You must be logged in to post a comment.