Zooming out, 2

Posted on January 16, 2021 by rpflee

In this morning’s dream, I could hold my lucid dream without feeling a headache. I felt comfortable as awake.

I was in a city and listening to an Inception-style music.

I tried to fold the city as in Inception so that I could have walked on a vertical land.

However, it did not work. The city got folded together, not as an L shape, [?]but as an L with a horizontal line head shape.[?]

Then I got myself waking up by flying-falling downwards.

— Me@2011.08.03

機遇創生論, 2.1

Posted on January 15, 2021 by rpflee

這段改編自 2010 年 4 月 18 日的對話。

不行。雖然尚算準確，但是不夠精采。

還有，「人生攻略理論」令人聯想到很多東西，而大部分也不是，我們那個合體大理論的內容。

「緣份攻略」都不行，因為感覺有點怪。

（安：那就不如叫做「緣份理論」。）

「理論」很空泛。不應把「理論」，視為名字的一部分。

（安：不如叫做「超級種子理論」，或者「廣義種子理論」？）

種子論最終定版？

種子論傳 …

種子論 X 傳 …

字母 X 可代表，前中後左中右上下東南西北，例如，種子論前傳、種子論左傳等等。原本的種子論，就為之正傳，種子正傳。即是好像 Microsoft DirectX 可以代表 Direct3D、DirectDraw、DirectMusic、DirectPlay、DirectSound 等等。.

但是「種子 X 傳」相當「拗口」，讀法不暢順。

（安：無錯，那相當「拗口」。)

大種子論？

（安：我剛才都是想到「大種子論」。）

但是，大的是理論，而不是種子。

種子大論？

（安：但「種子大論」比較奇怪。）

都是「大種子論」比較好一點。還有，遲一些有更大的理論時，可以叫做，巨大種子論、超巨大種子論、特超巨大種子論等等。

— Me@2021-01-13 04:52:02 PM

2006, 4

Posted on January 10, 2021 by rpflee

— Me@2021-01-10 06:11:40 PM

Ex 1.14 Lagrange equations for L’, 2

Posted on January 9, 2021 by rpflee

Structure and Interpretation of Classical Mechanics

Show by direct calculation that the Lagrange equations for $\displaystyle{L'}$ are satisfied if the Lagrange equations for $\displaystyle{L}$ are satisfied.

~~~

$\displaystyle{x = F(t, x')}$

$\displaystyle{x' = G(t, x)}$

$\displaystyle{ \begin{aligned} &\partial_2 L \circ \Gamma[q] \\ &= \frac{\partial}{\partial v} L(t, x, v) \\ &= \frac{\partial}{\partial v} L'(t, x', v') \\ &= \frac{\partial}{\partial x'} L'(t, x', v') \frac{\partial x'}{\partial v} + \frac{\partial}{\partial v'} L'(t, x', v') \frac{\partial v'}{\partial v} \\ &= \frac{\partial}{\partial v'} L'(t, x', v') \frac{\partial v'}{\partial v} \\ \end{aligned}}$

$\displaystyle{v' = \partial_0 G(t, x) + \partial_1 G(t,x) v}$

$\displaystyle{ \begin{aligned} \frac{\partial v'}{\partial v} &= \partial_1 G(t,x) = \frac{\partial x'}{\partial x} \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} &\partial_2 L \circ \Gamma[q] \\ &= \frac{\partial L'}{\partial v'} \frac{\partial x'}{\partial x} \\ \end{aligned}}$

The Lagrange equation:

$\displaystyle{ \begin{aligned} D ( \partial_2 L \circ \Gamma[q]) - (\partial_1 L \circ \Gamma[q]) &= 0 \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} &\partial_1 L \circ \Gamma[q] \\ &= \partial_1 L' \circ \Gamma[q'] \\ &= \frac{\partial}{\partial x} L' (t, x', v') \\ &= \frac{\partial L'}{\partial x'} \frac{\partial x'}{\partial x} + \frac{\partial L'}{\partial v'} \frac{\partial v'}{\partial x} \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} D ( \partial_2 L \circ \Gamma[q]) - (\partial_1 L \circ \Gamma[q]) &= 0 \\ D \left( \frac{\partial L'}{\partial v'} \frac{\partial x'}{\partial x} \right) - \left( \frac{\partial L'}{\partial x'} \frac{\partial x'}{\partial x} + \frac{\partial L'}{\partial v'} \frac{\partial v'}{\partial x} \right) &= 0 \\ D \left( \frac{\partial L'}{\partial v'} \right) \frac{\partial x'}{\partial x} + \frac{\partial L'}{\partial v'} D \left( \frac{\partial x'}{\partial x} \right) - \left( \frac{\partial L'}{\partial x'} \frac{\partial x'}{\partial x} + \frac{\partial L'}{\partial v'} \frac{\partial v'}{\partial x} \right) &= 0 \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} &D \left( \frac{\partial x'}{\partial x} \right) \\ &= \frac{d}{dt} \left( \frac{\partial x'}{\partial x} \right) \\ &= \frac{\partial}{\partial t} \left( \frac{\partial x'}{\partial x} \right) \frac{\partial t}{\partial t} + \frac{\partial}{\partial x'} \left( \frac{\partial x'}{\partial x} \right) \frac{\partial x'}{\partial t} + \frac{\partial}{\partial v'} \left( \frac{\partial x'}{\partial x} \right) \frac{\partial v'}{\partial t} \\ &= \frac{\partial}{\partial t} \left( \frac{\partial x'}{\partial x} \right) + \frac{\partial}{\partial x} \left( \frac{\partial x'}{\partial x'} \right) \frac{\partial x'}{\partial t} + \frac{\partial}{\partial x} \left( \frac{\partial x'}{\partial v'} \right) \frac{\partial v'}{\partial t} \\ &= \frac{\partial}{\partial t} \left( \frac{\partial x'}{\partial x} \right) + \frac{\partial}{\partial x} \left( 1 \right) \frac{\partial x'}{\partial t} + \frac{\partial}{\partial x} \left( 0 \right) \frac{\partial v'}{\partial t} \\ &= \frac{\partial}{\partial x} \left( \frac{\partial x'}{\partial t} \right) + 0 + 0 \\ &= \frac{\partial v'}{\partial x} \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} \left[ D \left( \frac{\partial L'}{\partial v'} \right) - \frac{\partial L'}{\partial x'} \right] \frac{\partial x'}{\partial x} + \frac{\partial L'}{\partial v'} \frac{\partial v'}{\partial x} - \frac{\partial L'}{\partial v'} \frac{\partial v'}{\partial x} &= 0 \\ \left[ D \left( \frac{\partial L'}{\partial v'} \right) - \frac{\partial L'}{\partial x'} \right] \frac{\partial x'}{\partial x} &= 0 \\ D \left( \frac{\partial L'}{\partial v'} \right) - \frac{\partial L'}{\partial x'} &= 0 \\ \end{aligned}}$

— Me@2021-01-06 08:10:46 PM

The square root of the probability, 4.3

Posted on January 6, 2021 by rpflee

Eigenstates 3.4.3

The indistinguishability of cases is where the quantum probability comes from.

— Me@2020-12-25 06:21:48 PM

In the double slit experiment, there are 4 cases:

1. only the left slit is open

2. only the right slit is open

3. both slits are open and a measuring device is installed somewhere in the experiment setup so that we can know which slit each photon passes through

4. both slits are open but no measuring device is installed; so for each photon, we have no which-way information

For simplicity, we rephrase the case-3 and case-4:

1. only the left slit is open

2. only the right slit is open

3. both slits are open, with which-way information

4. both slits are open, without which-way information

Case-3 can be regarded as a classical overlapping of case-1 and case-2, because if you check the result of case-3, you will find that it is just an overlapping of result case-1 and result case-2.

However, case-4 cannot be regarded as a classical overlapping of case-1 and case-2. Instead, case-4 is a quantum superposition. A quantum superposition canNOT be regarded as a classical overlapping of possibilities/probabilities/worlds/universes.

Experimentally, no classical overlapping can explain the interference pattern, especially the destruction interference part. An addition of two non-zero probability values can never result in a zero.

Logically, case-4 is a quantum superposition of go-left and go-right. Case-4 is neither AND nor OR of the case-1 and case-2.

We can discuss AND or OR only when there are really 2 distinguishable cases. Since there are not any kinds of measuring devices (for getting which-way information) installed anywhere in the case-4, go-left and go-right are actually indistinguishable cases. In other words, by defining case-4 as a no-measuring-device case, we have indirectly defined that go-left and go-right are actually indistinguishable cases, even in principle.

Note that saying “they are actually indistinguishable cases, even in principle” is equivalent to saying that “they are logically indistinguishable cases” or “they are logically the same case“. So discussing whether a photon has gone left or gone right is meaningless.

If 2 cases are actually indistinguishable even in principle, then in a sense, there is actually only 1 case, the case of “both slits are open but without measuring device installed anywhere” (case-4). Mathematically, this case is expressed as the quantum superposition of go-left and go-right.

Since it is only 1 case, it is meaningless to discuss AND or OR. It is neither “go-left AND go-right” nor “go-left OR go-right“, because the phrases “go-left” and “go-right” are themselves meaningless in this case.

— Me@2020-12-19 10:38 AM

— Me@2020-12-26 11:02 AM

It is a quantum superposition of go-left and go-right.

Quantum superposition is NOT an overlapping of worlds.

Quantum superposition is neither AND nor OR.

— Me@2020-12-26 09:07:22 AM

When the final states are distinguishable you add probabilities:

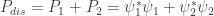
$\displaystyle{P_{dis} = P_1 + P_2 = \psi_1^*\psi_1 + \psi_2^*\psi_2}$

.

When the final state are indistinguishable,[^2] you add amplitudes:

$\displaystyle{\Psi_{1,2} = \psi_1 + \psi_2}$

and

$\displaystyle{P_{ind} = \Psi_{1,2}^*\Psi_{1,2} = \psi_1^*\psi_1 + \psi_1^*\psi_2 + \psi_2^*\psi_1 + \psi_2^*\psi_2}$

.

[^2]: This is not precise, the states need to be “coherent”, but you don’t want to hear about that today.

edited Mar 21 ’13 at 17:04
answered Mar 21 ’13 at 16:58

dmckee

— Physics Stack Exchange

.

$\displaystyle{ P_{ind} = P_1 + P_2 + \psi_2^*\psi_1 + \psi_2^*\psi_2 }$

$\displaystyle{ P_{\text{indistinguishable}} = P_{\text{distinguishable}} + \text{interference terms} }$

— Me@2020-12-26 09:07:46 AM

interference terms ~ indistinguishability effect

— Me@2020-12-26 01:22:36 PM

WHY NOT

Posted on January 5, 2021 by rpflee

You have only ONE life in this life.

WHY NOT do something extraordinary in order to help people to help others?

— Me@~2008

鐵達尼極限 2

Posted on January 5, 2021 by rpflee

尋覓 1.4

這段改編自 2010 年 10 月 14 日的對話。

對於沒有自己人生目標的人來說，

愛情有如患精神病，過不了「鐵達尼極限」（三日）。

— 黃子華

然後，又再深一層。

如果你要愛情事業成功，首先要令到自己，不需要愛情。

比喻說，如果你吃雪糕的原因是，你上了癮的話，吃雪糕就只能令你避免，暫時的不安，但不可以令你得到，真正的快樂。相反，如果你根本沒需要吃雪糕，而選擇吃雪糕，純粹是出於自由意志的話，你就可以真正享受得到，吃雪糕的樂趣。

那如何訓練到，自己不需要愛情呢？

剛才所講，

各人的心靈腦海之中，其實都有超過一個自己。只不過，眾多自我被困於，同一個頭顱之中。

如果你自己的眾多自我，也相處融洽時，你就不太需要外在愛情。相反，如果他們水火不容時，你就極有需要有愛情，用來逃避自己心中，那些眾多不友善的自我。

自己都不愛怎麼相愛怎麼可給愛人好處　– 林夕

人為什麼要有同伴？

比喻說，人自己一個時，太過孤獨，太過冰冷，所以，期望透過有同伴，去感受溫暖。

根據哲學家叔本華所講，人有如「寒冬裡的刺蝟」：一方面，牠們要走近對方，互相取暖；另一方面，走得太近，又會刺傷對方。

但是，如果有一個人，心中有一個太陽，自己會發熱發亮的話，他就不怕人情冷暖。亦即是話，如果你一個人時，生活已經十分精采的話，你就不需要愛情。

留意，「不需要」不代表「不應有」。一個人不需要愛情，而仍然選擇愛情的話，可以是因為技術上的問題，例如，剛巧有對象與他相愛，而他又想有自己的兒女。

Enjoy everything, need nothing, …

.

… especially for human relationships.

– Conversations with God

— Me@2021-01-03 04:18:55 PM

1954

Posted on January 2, 2021 by rpflee

— Photomyne colorization

— Me@2021-01-02 05:20:52 PM

Problem 2.5a

Posted on January 1, 2021 by rpflee

A First Course in String Theory

2.5 Constructing simple orbifolds

(a) Consider a circle $\displaystyle{S^1}$ , presented as the real line with the identification $\displaystyle{x \sim x + 2}$ . Choose $\displaystyle{-1 < x \le 1}$ as the fundamental domain. The circle is the space $\displaystyle{-1 < x \le 1}$ with points $\displaystyle{x = \pm 1}$ identified. The orbifold $\displaystyle{S^1/\mathbb{Z}_2}$ is defined by imposing the (so-called) $\displaystyle{\mathbb{Z}_2}$ identification $\displaystyle{x \sim -x}$ . Describe the action of this identification on the circle. Show that there are two points on the circle that are left fixed by the $\displaystyle{\mathbb{Z}_2}$ action. Find a fundamental domain for the two identifications. Describe the orbifold $\displaystyle{S^1/\mathbb{Z}_2}$ in simple terms.

~~~

Put point $\displaystyle{x=0}$ and point $\displaystyle{x=1}$ on the positions that they can form a horizontal diameter.

Then the action is a reflection of the lower semi-circle through the horizontal diameter to the upper semi-circle.

Point $\displaystyle{x=0}$ and point $\displaystyle{x=1}$ are the two fixed points.

A possible fundamental domain is $\displaystyle{0 \le x \le 1}$ .

If a variable point $\displaystyle{x}$ moves from 0 to 1 and then keeps going, that point will actually go back and forth between 0 and 1.

— Me@2020-12-31 04:43:07 PM

The square root of the probability, 4.2

Posted on December 30, 2020 by rpflee

Eigenstates 3.4.2

The difference between quantum and classical is due to the indistinguishability of cases.

— Me@2020-12-26 01:25:03 PM

Statistical effects of indistinguishability

The indistinguishability of particles has a profound effect on their statistical properties.

The differences between the statistical behavior of fermions, bosons, and distinguishable particles can be illustrated using a system of two particles. The particles are designated A and B. Each particle can exist in two possible states, labelled $\displaystyle{ |0 \rangle }$ and $\displaystyle{|1\rangle}$ , which have the same energy.

The composite system can evolve in time, interacting with a noisy environment. Because the $\displaystyle{|0\rangle}$ and $\displaystyle{|1\rangle}$ states are energetically equivalent, neither state is favored, so this process has the effect of randomizing the states. (This is discussed in the article on quantum entanglement.) After some time, the composite system will have an equal probability of occupying each of the states available to it. The particle states are then measured.

If A and B are distinguishable particles, then the composite system has four distinct states: $\displaystyle{|0\rangle |0\rangle}$ , $\displaystyle{|1\rangle |1\rangle}$ , $\displaystyle{ |0\rangle |1\rangle}$ , and $\displaystyle{|1\rangle |0\rangle }$ . The probability of obtaining two particles in the $\displaystyle{|0\rangle}$ state is 0.25; the probability of obtaining two particles in the $\displaystyle{|1\rangle}$ state is 0.25; and the probability of obtaining one particle in the $\displaystyle{|0\rangle}$ state and the other in the $\displaystyle{|1\rangle}$ state is 0.5.

If A and B are identical bosons, then the composite system has only three distinct states: $\displaystyle{|0\rangle |0\rangle}$ , $\displaystyle{ |1\rangle |1\rangle }$ , and $\displaystyle{{\frac {1}{\sqrt {2}}}(|0\rangle |1\rangle +|1\rangle |0\rangle)}$ . When the experiment is performed, the probability of obtaining two particles in the $\displaystyle{|0\rangle}$ is now 0.33; the probability of obtaining two particles in the $\displaystyle{|1\rangle}$ state is 0.33; and the probability of obtaining one particle in the $\displaystyle{|0\rangle}$ state and the other in the $\displaystyle{|1\rangle}$ state is 0.33. Note that the probability of finding particles in the same state is relatively larger than in the distinguishable case. This demonstrates the tendency of bosons to “clump.”

If A and B are identical fermions, there is only one state available to the composite system: the totally antisymmetric state $\displaystyle{{\frac {1}{\sqrt {2}}}(|0\rangle |1\rangle -|1\rangle |0\rangle)}$ . When the experiment is performed, one particle is always in the $\displaystyle{|0\rangle}$ state and the other is in the $\displaystyle{|1\rangle}$ state.

The results are summarized in Table 1:

— Wikipedia on Identical particles

Cheer up?

Posted on December 30, 2020 by rpflee

What you encourage people, don’t say “don’t worry, be happy” or “cheer up”.

They are nonsense, because they are not actionable.

What I really need to know is HOW to be happy.

What I really need to know is what ACTION to take to solve my problem.

When you see a doctor, what if, without giving any other advice, he just tells you to “cheer up”?

在開解朋友時，千萬不要講「加油」和「睇開啲啦」等廢話。

那只會令當事人，更加不開心。

— Me@2011.06.26

— Me@2020-12-30

機遇創生論 1.7.2

Posted on December 29, 2020 by rpflee

因果律 2.2

這個大統一理論的成員，包括（但不止於）：

精簡圖：

種子論
反白論
間書原理
完備知識論

自由決定論

它們可以大統一的成因，在於它們除了各個自成一國外，還可以合體理解和應用。

「自由意志」問題方面，如果要討論的話，要先釐清「人有沒有自由意志」的意思，因為，它有超過一個常用的詮釋：

1. 思：

人可不可以控制到，自己的「思想意志」？

如果可以的話，

2. 因：

人（的自由思想，）可不可以控制到，自己身體的行動？

如果可以的話，

3. 果：

人（的自由行動，）可不可以控制到，自己人生（或者世界歷史）的發展大方向？

詳細一點的版本是：

1. 思：

意志有沒有自由？

究竟人的思想是有自由？還是其實，人的思想受制於教育等外在因素，所以都是不由自主的呢？

那就有如機械人的思想般，其實只是根據程式碼來運行。

2. 因：

即使假設意志有自由，人的身體是物體，它的運行仍然，受著物理力學定律所主宰，理應沒有自由。

在「Laplace 因果律」的觀點下，兩者其實又沒有分別，因為「意志」都是，受物理定律的支配。「思想」是腦部的狀態，而腦部的生物化學作用，最底層也其實是，由物理定律控制。

如果「Laplace 因果律」正確的話，人或者任何其他東西，也沒有自由。

至於「Laplace 因果律」正確與否，和人有自由與否，在我們以前的討論中，已得出了結論：

「自由論」和「決定論」，其實沒有實質上的分別。

所以，我把這個理論，稱為「自由決定論」。

如果對「因果律」和「自由意志」話題有興趣，想知道這結論的理據的話，請在本網誌搜尋「因果律」。

— Me@2020-12-29 05:46:05 PM

1994

Posted on December 29, 2020 by rpflee

This was my Art result. I had a great art teacher Mr Lo in that year. He taught us a lot of design concepts.

— Me@2020-12-29 10:52:04 AM

Ex 1.14 Lagrange equations for L’

Posted on December 28, 2020 by rpflee

Structure and Interpretation of Classical Mechanics

Show by direct calculation that the Lagrange equations for $\displaystyle{L'}$ are satisfied if the Lagrange equations for $\displaystyle{L}$ are satisfied.

~~~

Equation (1.69):

$\displaystyle{C \circ \Gamma[q'] = \Gamma[q]}$

Equation (1.70):

$\displaystyle{L' = L \circ C}$

Equation (1.71):

$\displaystyle{L' \circ \Gamma[q'] = L \circ C \circ \Gamma[q'] = L \circ \Gamma[q]}$

The Lagrange equation:

$\displaystyle{ \begin{aligned} D ( \partial_2 L \circ \Gamma[q]) - (\partial_1 L \circ \Gamma[q]) &= 0 \\ \end{aligned}}$

Since it is just a coordinate transformation $\displaystyle{x = F(t, x')}$ , $\displaystyle{x}$ has no explicitly dependent on $\displaystyle{v'}$ . Similarly, if we consider the coordinate transformation $\displaystyle{x' = G(t, x)}$ , $\displaystyle{x'}$ has no explicitly dependent on $\displaystyle{v}$ . So

$\displaystyle{ \begin{aligned} \frac{\partial x'}{\partial v} &= 0 \\ \end{aligned}}$

$\displaystyle{ \begin{aligned} &\partial_2 L \circ \Gamma[q] \\ &= \frac{\partial}{\partial v'} L'(t, x', v') \frac{\partial v'}{\partial v} \\ \end{aligned}}$

…

— Me@2020-12-28 04:03:24 PM

The square root of the probability, 4

Posted on December 27, 2020 by rpflee

Eigenstates 3.4

quantum ~ classical with the indistinguishability of cases

— Me@2020-12-23 06:19:00 PM

In statistical mechanics, a semi-classical derivation of the entropy that does not take into account the indistinguishability of particles, yields an expression for the entropy which is not extensive (is not proportional to the amount of substance in question). This leads to a paradox known as the Gibbs paradox, after Josiah Willard Gibbs who proposed this thought experiment in 1874‒1875. The paradox allows for the entropy of closed systems to decrease, violating the second law of thermodynamics. A related paradox is the “mixing paradox”. If one takes the perspective that the definition of entropy must be changed so as to ignore particle permutation, the paradox is averted.

— Wikipedia on Gibbs paradox

Beauty and the Beast, 2

Posted on December 25, 2020 by rpflee

Beauty 7

Beauty is the goal, but may not be the mean.

— Me@2020-10-29 08:29:31 AM

The path to beauty may not be itself beautiful.

— Me@2020-11-03 11:32:52 AM

尋覓 1.3

Posted on December 25, 2020 by rpflee

這段改編自 2010 年 10 月 14 日的對話。

…

但是，十年後的物理三十歲，一個的心理年齡已，發展到三十五歲，而另一個的心理，卻仍然停留在二十五歲。那樣的話，二人的感情，就未必再能維持。

除了相遇那年要夾（融洽）外，還要在之後的每一年，也是那樣夾。換句話說，即是兩人的變法要配合。所以，難度其實深了一層。

然後，再深一層。其實呢，在看《潛行凶間》之前，我已有這個知識：

就算只考慮「現在的你」，或者「現在的他」，各人的心靈腦海之中，其實都有超過一個自己。只不過，眾多自我被困於，同一個頭顱之中。

最簡單的講法是，每人也起碼有兩個自己。

左腦的性格，和右腦的性格，其實是不同的。左腦喜歡計數邏輯思考，右腦鍾情音樂藝術創作。

實情是，每一個人，也擁有超過兩個自己。簡單起見，假設你只有「甲、乙、丙」三個自己；而你的潛在情人，也只有「A、B、C」三個人格。那樣，你和他要完全夾的話，那就需要那九對組合也夾才可以。

1. 甲A

2. 甲B

3. 甲C

4. 乙A

5. 乙B

6. 乙C

7. 丙A

8. 丙B

9. 丙C

那為什麼拍拖那時，通常很開心？而結婚後，通常也不會太開心？

那是因為，拍拖時，通常只有「最好的你」和「最好的他」相處。結婚後，你會發現，原來在他的頭顱中，除了「最好的他」之外，還有很多隻怪獸。

友情方面，你可以選擇，只要對方的優點；
愛情方面，你不可以選擇，不要對方的缺點。

— Me@2010.06.01

友情方面，你可以選擇，只要對方最好的優點；
愛情方面，你不可以選擇，不要對方最差的缺點。

–- Me@2010.06.01

.

因為

朋友，只需接受部分；
情人，卻需接受全部。

— Me@2010.06.07

這就是我上次講，《潛行凶間》的劇情。《潛行凶間》的內容，有七成是真實的。

整體而言，今天的分手，對你來說，利遠大於弊，因為，他是你將來結婚對象的機會，實在太微；早分為妙。

— Me@2020-12-23 10:39:26 PM

1980s, 2

Posted on December 22, 2020 by rpflee

— Photomyne colorization

— Me@2020-12-22 04:39:33 PM

Problem 2.4

Posted on December 21, 2020 by rpflee

A First Course in String Theory

2.4 Lorentz transformations as matrices

A matrix L that satisfies (2.46) is a Lorentz transformation. Show the following.

(b) If $\displaystyle{L}$ is a Lorentz transformation so is the inverse matrix $\displaystyle{L^{-1}}$ .

~~~

(b)

$\displaystyle{ \begin{aligned} (\mathbf{A}^\mathrm{T})^{-1} &= (\mathbf{A}^{-1})^\mathrm{T} \\ L^T \eta L &= \eta \\ \eta &= [L^T]^{-1} \eta L^{-1} \\ [L^T]^{-1} \eta L^{-1} &= \eta \\ [L^{-1}]^T \eta L^{-1} &= \eta \\ \end{aligned}}$

(c)

$\displaystyle{ \begin{aligned} L^T \eta L &= \eta \\ (L^T \eta L)^{-1} &= (\eta)^{-1} \\ L^{-1} \eta^{-1} (L^T)^{-1} &= \eta \\ L^{-1} \eta (L^T)^{-1} &= \eta \\ \eta &= L \eta L^T \\ L \eta L^T &= \eta \\ \end{aligned}}$

— Me@2020-12-21 04:24:33 PM

Pointer state, 3

Posted on December 18, 2020 by rpflee

Eigenstates 3.3 | The square root of the probability, 3

In calculation, if a quantum state is in a superposition, that superposition is a superposition of eigenstates.

However, real superposition does not just include eigenstates that make macroscopic senses.

That is the major mistake of the many-worlds interpretation of quantum mechanics.

— Me@2017-12-30 10:24 AM

— Me@2018-07-03 07:24 PM

— Me@2020-12-18 06:12 PM

Mathematically, a quantum superposition is a superposition of eigenstates. An eigenstate is a quantum state that is corresponding to a macroscopic state. A superposition state is a quantum state that has no classical correspondence.

The macroscopic states are the only observable states. An observable state is one that can be measured directly or indirectly. For an unobservable state, we write it as a superposition of eigenstates. We always write a superposition state as a superposition of observable states; so in this sense, before measurement, we can almost say that the system is in a superposition of different (possible) classical macroscopic universes.

However, conceptually, especially when thinking in terms of Feynman’s summing over histories picture, a quantum state is more than a superposition of classical states. In other words, a system can have a quantum state which is a superposition of not only normal classical states, but also bizarre classical states and eigen-but-classically-impossible states.

A bizarre classical state is a state that follows classical physical laws, but is highly improbable that, in daily life language, we label such a state “impossible”, such as a human with five arms.

An eigen-but-classically-impossible state is a state that violates classical physical laws, such as a castle floating in the sky.

For a superposition, if we allow only normal classical states as the component eigenstates, a lot of the quantum phenomena, such as quantum tunnelling, cannot be explained.

If you want multiple universes, you have to include not only normal universes, but also the bizarre ones.

Actually, even for the double-slit experiment, “superposition of classical states” is not able to explain the existence of the interference patterns.

The superposition of the electron-go-left universe and the electron-go-right universe does not form this universe, where the interference patterns exist.

— Me@2020-12-16 05:18:03 PM

One of the reasons is that a quantum superposition is not a superposition of different possibilities/probabilities/worlds/universes, but a superposition of quantum eigenstates, which, in a sense, are square roots of probabilities.

— Me@2020-12-18 06:07:22 PM

Physics Town

continues